题目内容
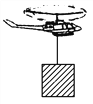
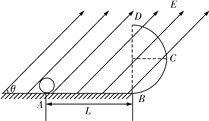
【题目】如图所示,竖直平面内的![]() 圆弧形光滑管道半径略大于小球半径,管道中心到圆心距离为R,A点与圆心O等高,AD为水平面,B点在O的正下方,小球自A点正上方由静止释放,自由下落至A点时进入管道,当小球到达B点时,管壁对小球的弹力大小为小球重力大小的9倍,求:
圆弧形光滑管道半径略大于小球半径,管道中心到圆心距离为R,A点与圆心O等高,AD为水平面,B点在O的正下方,小球自A点正上方由静止释放,自由下落至A点时进入管道,当小球到达B点时,管壁对小球的弹力大小为小球重力大小的9倍,求:
(1)释放点距A点的竖直高度;
(2)落点C与A的水平距离。

【答案】(1)3R;(2)(2![]() -1)R.;
-1)R.;
【解析】(1)设小球到达B点的速度为v1.因为到达B点时管壁对小球的弹力大小为小球重力大小的9倍,所以有
9mg-mg=m![]()
又由机械能守恒定律得mg(h+R)=![]() mv12
mv12
由此可解得h=3R.
(2)设小球到达最高点的速度为v2,落点C与A的水平距离为x.
由机械能守恒定律得![]() mv12=
mv12=![]() mv22+2mgR
mv22+2mgR
由平抛运动规律得R=![]() gt2,R+x=v2t
gt2,R+x=v2t
由此可解得x=(2![]() -1)R.
-1)R.

练习册系列答案
相关题目