题目内容
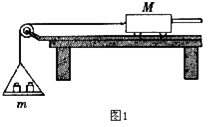
【题目】如图所示,固定斜面足够长,斜面与水平面的夹角α=30°,一质量为3m的“L”型工件沿斜面以速度v0匀速向下运动,工件上表面光滑,下端为挡板.某时,一质量为m的小木块从工件上的A点,沿斜面向下以速度v0滑上工件,当木块运动到工件下端时(与挡板碰前的瞬间),工件速度刚好减为零,后木块与挡板第1次相碰,以后每隔一段时间,木块就与工件挡板碰撞一次,已知木块与挡板都是弹性碰撞且碰撞时间极短,木块始终在工件上运动,重力加速度为g,求: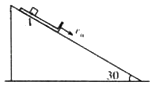
(1)木块滑上工件时,木块、工件各自的加速度大小;
(2)木块与挡板第1次碰撞后的瞬间,木块、工件各自的速度大小;
(3)木块与挡板第1次碰撞至第n(n=2,3,4,5,…)次碰撞的时间间隔及此时间间隔内木块和工件组成的系统损失的机械能△E.
【答案】
(1)
解:设工件与斜面间的动摩擦因数为μ,木块加速度为a1,工件的加速度为a2.
根据牛顿第二定律得:
对木块:mgsinα=ma1.
对工件:μ(3m+m)gcosα﹣3mgsinα=3ma2.
工件匀速运动时,由平衡条件得:μ3mgcosα=3mgsinα
解得 a1= ![]() ,a2=
,a2= ![]()
(2)
解:设碰挡板前木块的速度为v,取沿斜面向下为正方向为正方向,由动量守恒定律得:
3mv0+mv0=mv
得 v=4v0.
木块以速度v与挡板发生弹性碰撞,设碰后木块的速度为v1,工件的速度为v2,由动量守恒定律得:
mv=mv1+3mv2.
由能量守恒得:
![]() mv2=
mv2= ![]() mv12+
mv12+ ![]() 3mv22.
3mv22.
解得 v1=﹣2v0,v2=2v0
(3)
解:第1次碰撞后,木块以2v0沿工件向上匀减速运动,工件以2v0沿斜面向下匀减速运动,工件速度再次减为零的时间
t= ![]() =
= ![]()
木块的速度 v1′=﹣2v0+a1t=4v0.
此时,木块的位移 x1=﹣2v0t+ ![]() =
= ![]()
工件的位移 x2=2v0t﹣ ![]() =
= ![]()
即木块、工件第2次相碰前瞬间的速度与第1交相碰前的瞬间速度相同,以后木块、工件重复前面的运动过程,则第1次与第n次碰撞的时间间隔
△t=(n﹣1)t= ![]() ,(n=2,2,3,4,…)
,(n=2,2,3,4,…)
木块、工件每次碰撞时,木块和工件的总动能都相等,△t时间内木块、工件减少的机械能等于木块、工件减少的重力势能.
△E=4mg(n﹣1)x2sin30°
解得△E=24(n﹣1)mv02,(n=2,2,3,4,…)
【解析】(1)运用隔离法,根据牛顿第二定律求木块、工件各自的加速度大小;(2)由动量守恒定律求出碰挡板前木块的速度,由动量守恒定律和能量守恒定律求木块与挡板第1次碰撞后的瞬间,木块、工件各自的速度大小;(3)第1次碰撞后,木块以2v0沿工件向上匀减速运动,工件以2v0沿斜面向下匀减速运动,根据速度公式求工件速度再次减为零的时间,并由位移公式求出位移.木块、工件第2次相碰前瞬间的速度与第1交相碰前的瞬间速度相同,以后木块、工件重复前面的运动过程,再求得第1次与第n次碰撞的时间间隔.此时间间隔内木块和工件组成的系统损失的机械能△E等于木块、工件减少的重力势能.
【考点精析】本题主要考查了功能关系和动量守恒定律的相关知识点,需要掌握当只有重力(或弹簧弹力)做功时,物体的机械能守恒;重力对物体做的功等于物体重力势能的减少:W G =E p1 -E p2;合外力对物体所做的功等于物体动能的变化:W 合 =E k2 -E k1 (动能定理);除了重力(或弹簧弹力)之外的力对物体所做的功等于物体机械能的变化:W F =E 2 -E 1;动量守恒定律成立的条件:系统不受外力或系统所受外力的合力为零;系统所受的外力的合力虽不为零,但系统外力比内力小得多;系统所受外力的合力虽不为零,但在某个方向上的分量为零,则在该方向上系统的总动量的分量保持不变才能正确解答此题.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案