��Ŀ����
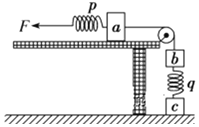
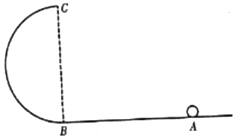
����Ŀ����ͼ��ʾ���뾶ΪR���ڲ��⻬�İ�Բ�ι��BC�̶���ˮƽ���ϣ���ˮƽ��������B�㣬һ����Ϊm��С���Գ��ٶ�v0�Ӿ���B��Ϊ2R��A�������˶������Բ�ι����С��ӹ����ߵ�C�뿪���ڿ�����ƽ���˶���ǡ����A����أ��������ٶ�Ϊg������˵����ȷ���ǣ�������
A. С������Բ�ι�����ڰ�Բ�ι������͵�B���Թ����ѹ������mg
B. С���ڰ�Բ�ι����ߵ�C���Թ����ѹ��Ϊmg
C. С���ڰ�Բ�ι����ߵ�C���Թ����ѹ��Ϊ0
D. С�����ʱ�ٶȷ�����ˮƽ����нǵ�����ֵΪ2
���𰸡�CD
��������
�뿪C����ƽ���˶�������ֱ����
![]()
ˮƽ����
2R��vCt
��ã�
![]()
��C����ţ�ٵڶ����ɵã�
F+mg��![]()
��ã�
F��0
��ţ�ٵ�������֪�Թ����ѹ��Ϊ0����С�����ʱ�ٶȷ�����ˮƽ����н�Ϊ������
![]()
��B��C�Ĺ����ɶ��ܶ����ã�
��mg2R=![]()
����͵�B����ţ�ٵڶ����ɵã�
F��mg��m![]()
������ã�
F��6mg
��ţ�ٵ�������֪�Թ����ѹ������6mg
A. С������Բ�ι�����ڰ�Բ�ι������͵�B���Թ����ѹ������mg�������������A�������ⲻ�����
B. С���ڰ�Բ�ι����ߵ�C���Թ����ѹ��Ϊmg�������������B�������ⲻ�����
C. С���ڰ�Բ�ι����ߵ�C���Թ����ѹ��Ϊ0������������C�������������
D. С�����ʱ�ٶȷ�����ˮƽ����нǵ�����ֵΪ2������������D�������������

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�