题目内容
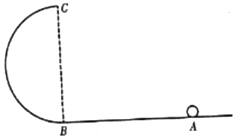
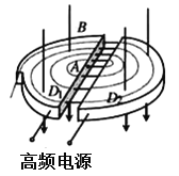
【题目】如图1所示为回旋加速器的示意图。它由两个铝制D型金属扁盒组成，两个D形盒正中间开有一条狭缝，两个D型盒处在匀强磁场中并接在高频交变电源上。在
盒中心A处有离子源，它产生并发出的
粒子，经狭缝电压加速后，进入
盒中。在磁场力的作用下运动半个圆周后，再次经狭缝电压加速。为保证粒子每次经过狭缝都被加速，设法使交变电压的周期与粒子在狭缝及磁场中运动的周期一致如。此周而复始，速度越来越大，运动半径也越来越大，最后到达D型盒的边缘，以最大速度被导出。已知粒子电荷量为q质量为m，加速时电极间电压大小恒为U,磁场的磁感应强度为B，D型盒的半径为R.设狭缝很窄，粒子通过狭缝的时间可以忽略不计，且粒子从离子源发出时的初速度为零。(不计粒子重力)求：
(1)粒子第1次由盒进入盒中时的速度大小；
(2)粒子被加速后获得的最大动能
；
(3)符合条件的交变电压的周期T；
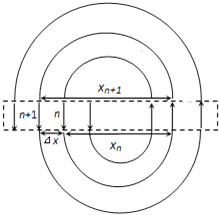
(4)粒子仍在盒中活动过程中，粒子在第n次由盒进入盒与紧接着第n+1次由盒进入盒位置之间的距离Δx.
【答案】（1）
（2）
（3）
（4）
【解析】
（1）设α粒子第一次被加速后进入D2盒中时的速度大小为v1，根据动能定理有
解得，
（2）α粒子在D形盒内做圆周运动，轨道半径达到最大时被引出，具有最大动能．设此时的速度为v，有
解得：
设α粒子的最大动能为Ek，则
解得：
（3）设交变电压的周期为T，为保证粒子每次经过狭缝都被加速，带电粒子在磁场中运动一周的时间应等于交变电压的周期（在狭缝的时间极短忽略不计），则交变电压的周期
（4）离子经电场第1次加速后，以速度v1进入D2盒，设轨道半径为r1
则 
离子经第2次电场加速后，以速度v2进入D1盒，设轨道半径为r2
则 
离子第n次由D1盒进入D2盒，离子已经过（2n-1）次电场加速，以速度v2n-1进入D2盒，由动能定理：
轨道半径
离子经第n+1次由D1盒进入D2盒，离子已经过2n次电场加速，以速度v2n进入D1盒，由动能定理：
轨道半径：
则△x=2（rn+1-rn）（如图所示）
解得，
