题目内容
【题目】某航天飞机在地球赤道上空飞行,轨道半径为r,飞行方向与地球的自转方向相同,设地球的自转角速度为ω0,地球半径为R,地球两极处的重力加速度为g,引力常量为G,在某时刻航天飞机通过赤道上某建筑物的上方,求:
(1)地球的密度;
(2)航天飞机绕地球转动的周期T;
(3)它下次通过该建筑物上方所需的时间。
【答案】(1)地球的密度![]() ;
;
(2)航天飞机绕地球转动的周期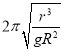 ;
;
(3)航天飞机的高度低于同步卫星的高度,所用时间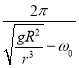 ;
;
航天飞机的高度高于同步卫星的高度,所用时间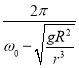 。
。
【解析】
根据航天飞机的万有引力等于向心力,列式求出周期和角速度表达式,航天飞机再次经过某建筑物上空时,比地球多转动或少转动一圈。
(1)地球表面的物体重力等于万有引力,有:![]() ,
,
解得:![]() ,
,
地球的密度为:![]() ;
;
(2)根据万有引力提供向心力,有:![]() ,
,
由于:![]() ,
,
联立解得: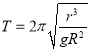 ;
;
(3)用ω表示航天飞机的角速度,若ω>ω0,即航天飞机的高度低于同步卫星的高度,用t表示所需的时间,则:
ωt﹣ω0t=2π,
解得: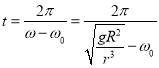 ;
;
若ω<ω0,即航天飞机的高度高于同步卫星的高度,用t表示所需的时间,则:
ω0t﹣ωt=2π,
解得: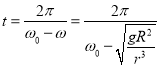 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目