Question

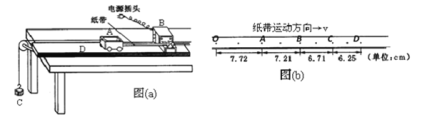
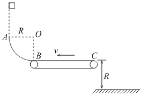
【题目】如图所示，竖直平面内的光滑四分之一圆弧轨道与水平传送带相切于B点，圆弧轨道的半径为R，传送带的长为2R，传送带上表面离地高也为R，传送带正以速度v=沿逆时针方向转动，一质量为m的物块在圆弧轨道的上端A上方某高度处由静止下落，刚好能从A点进入圆弧轨道，若物块与传送带间的动摩擦因数为=0.5，重力加速度为g，空气阻力不计，求：

(1)要使物块不能从传送带的右端滑离，物块从A点上方释放的高度应满足什么条件?

(2)若物块滑离传送带后落在地面上的位置离传送带右端C的水平距离为R，则物块在B点时对圆弧轨道的压力多大？

(3)若物块滑上传送带后刚好不能从传送带右端滑离则此种情况下，物块在传送带上运动的全过程中，传送带电动机因为物块在传送带上滑动额外做的功为多少?

Answer 1

【答案】（1）见解析（2） （3）

【解析】

（1）设当物块刚好不能从传送带的右端滑离时，物块从A点上方释放的高度为h，根据动能定理，则有：mg（h+R）-μmg2R=0；
解得：h=0
即要使物块不滑离传送带，物块不能从A点上方任一位置释放，只能从圆弧面上释放；
（2）设物块在C点的速度为vC，则R=vCt；
且R=gt2
设物块在B点的速度为vB，物块从B到C的过程中，根据动能定理，

μmg2R＝mvB2mvC2
解得：；
在B点，设圆弧轨道对物块的支持力为F，根据牛顿第二定律，则有：F-mg=m；
解得：F=mg
根据牛顿第三定律，物块在B点时对圆弧轨道的压力为F′=F=mg
（3）如果物块刚好能滑到传送带的右端，则物块到达C端时，速度为零，物块在B点速度为vB，则mvB2＝2μmgR，

解得：vB=
然后在摩擦力作用下，向左匀加速直线运动，速度达到v=与传送带一起匀速运动；因电动机额外做的功等于全过程中，皮带克服摩擦力做的功，则有：

W=μmgvt=；