Question

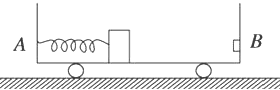
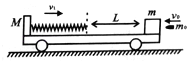
【题目】如图所示，光滑水平面上有一辆质量为M=1kg的小车，一轻弹簧固定在小车挡板上，此时弹簧长度恰好为原长，小车上表面的右端放置一个质量为m=0.9kg滑块（可视为质点），滑块与小车上表面间的动摩擦因数为μ=0.2，滑块与弹簧右端相距L=0.6m，整个系统一起以v1=10m/s的速度向右做匀速直线运动．现在有一质量为m0=0.1kg的子弹，以v0=150m/s的速度向左射入滑块且不穿出，所用时间极短．滑块在小车上运动一段距离后挤压弹簧，当弹簧压缩到最短时的压缩量为d=0.5m，g=10m/s2．求

①子弹刚射射入滑块时，子弹与滑块的共同速度；

②弹簧压缩到最短时，弹簧弹性势能的大小．

Answer 1

【答案】①6m/s ②61.8J

【解析】（1）子弹射入滑块后的共同速度大为v2，设向右为正方向，对子弹与滑块组成的系统应用动量守恒定律得：

①
解得： ②
方向向左；

（2）子弹，滑块与小车，三者的共同速度为v3，当三者达到共同速度时弹簧压缩量最大，弹性势能最大．由动量守恒定律得：

= ③
④
设最大弹性势能为，对三个物体组成的系统应用能量守恒定律
⑤
⑥
由⑤⑥两式解得 ⑦