题目内容
19. 在“利用单摆测重力加速度”的实验中
在“利用单摆测重力加速度”的实验中①测得摆线长lo,小球直径D,小球完成n次全振动的时间t,则实验测得的重力加速度的表达式g=$\frac{{4{π^2}({l_o}+\frac{D}{2}){n^2}}}{t^2}$;
②实验中如果重力加速度的测量值偏大,其可能的原因是C.
A.把摆线的长度lo当成了摆长
B.摆线上端未牢固地固定于O点,振动中出现松动,使摆线变长
C.测量周期时,误将摆球(n-1)次全振动的时间t记成了n次全振动的时间
D.摆球的质量过大
③为了减少实验误差,可采用图象法处理数据,通过多次改变摆长,测得多组摆长L和对应的周期T,并作出T2-L图象,如图所示.若图线的斜率为k,则用k表示重力加速度的测量值g=$\frac{4{π}^{2}}{k}$.
分析 ①单摆的周期是一次全振动的时间,由T=$\frac{t}{n}$求出周期.单摆的摆长等于摆线的长度加小球的半径.由单摆的周期公式求出g.
②根据g的表达式分析误差产生的原因.
③根据单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$变形得到,T2与L的表达式,再根据数学知识确定图象斜率的物理意义,即可求得g.
解答 解:①由题,单摆的周期为T=$\frac{t}{n}$.单摆的摆长L=l0+$\frac{D}{2}$.
由单摆的周期公式T=2π$\sqrt{\frac{L}{g}}$得,g=$\frac{{4{π^2}({l_o}+\frac{D}{2}){n^2}}}{t^2}$.
②由T=2π$\sqrt{\frac{L}{g}}$得,g=$\frac{4{π}^{2}L}{{T}^{2}}$
A、把摆线的长度lo当成了摆长,L变短,由上式可知,测得的g值偏小,故A错误.
B、摆线上端未牢固地固定于O点,振动中出现松动,使摆线变长,周期T变大,则g偏小,故B错误.
C、测量周期时,误将摆球(n-1)次全振动的时间t记成了n次全振动的时间,测出的周期T变小,则g偏大,故C正确.
D、单摆的周期与摆球的质量无关,故D错误.
故选:C
③由由T=2π$\sqrt{\frac{L}{g}}$得T2=$\frac{4{π}^{2}}{g}L$,由数学知识得知,T2-L图线的斜率k=$\frac{4{π}^{2}}{g}$,得 g=$\frac{4{π}^{2}}{k}$
故答案为:
(1)①$\frac{{4{π^2}({l_o}+\frac{D}{2}){n^2}}}{t^2}$.
②C.③$\frac{{4{π^2}}}{k}$.
点评 本题要掌握测量重力加速度的原理:单摆周期公式T=2π$\sqrt{\frac{L}{g}}$,根据实验原理分析误差产生的原因,结合数学知识图象的物理意义.

| A. | 雷雨天气外出时,可以在孤立的高大建筑物和大树下避雨 | |
| B. | 如果在旷野遭遇雷雨天气时,应立即蹲下,可以避免雷电的袭击 | |
| C. | 雷雨天气外出时,在户外打手机是安全的 | |
| D. | 以上做法都不正确 |
 如图所示,水平面上质量为10kg的木箱与墙角距离为$\frac{189}{8}$m,某人用F=125N的力,从静止开始推木箱,推力斜向下与水平方向成37°角,木箱与水平面之间的动摩擦因数为0.4.若推力作用一段时间t后撤去,木箱恰好能到达墙角处,则这段时间t为( ) (取sin37°=0.6,cos37°=0.8,g=10m/s2)
如图所示,水平面上质量为10kg的木箱与墙角距离为$\frac{189}{8}$m,某人用F=125N的力,从静止开始推木箱,推力斜向下与水平方向成37°角,木箱与水平面之间的动摩擦因数为0.4.若推力作用一段时间t后撤去,木箱恰好能到达墙角处,则这段时间t为( ) (取sin37°=0.6,cos37°=0.8,g=10m/s2)| A. | 3s | B. | $\frac{6}{5}$$\sqrt{5}$s | C. | $\frac{3}{10}$$\sqrt{70}$s | D. | $\frac{3}{2}$$\sqrt{7}$s |
| A. | 力 | B. | 时间 | C. | 长度 | D. | 速度 |
 如图所示,一均匀扁平条形磁铁与一线圈共面,磁铁中心与圆心O重合,下列运动中能使线圈中产生感应电流的是( )
如图所示,一均匀扁平条形磁铁与一线圈共面,磁铁中心与圆心O重合,下列运动中能使线圈中产生感应电流的是( )| A. | 磁铁不动,线圈在纸面内绕过O点的轴顺时针转动 | |
| B. | 线圈不动,磁铁在纸面内绕过O点的轴逆时针转动 | |
| C. | N极垂直纸面向里、S极垂直纸面向外,绕O点转动 | |
| D. | 线圈不动,磁铁沿垂直线圈平面过O的方向向纸面外运动 |
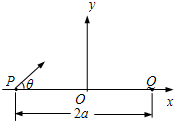 如图所示,平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P点以相同的速率斜向右上方的各个方向射出(即与x轴正方向的夹角θ,0°<θ<90°),经过某一个垂直于xoy平面向里、磁感应强度大小为B的有界匀强磁场区域后,最终会聚到Q点,这些微粒的运动轨迹关于y轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
如图所示,平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P点以相同的速率斜向右上方的各个方向射出(即与x轴正方向的夹角θ,0°<θ<90°),经过某一个垂直于xoy平面向里、磁感应强度大小为B的有界匀强磁场区域后,最终会聚到Q点,这些微粒的运动轨迹关于y轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
 将打点计时器接在电压为6V、频率为50Hz的交流电源上,自由下落的重物质量为1kg.如图所示为一条理想的纸带,单位是cm,g取9.8m/s2,O、A之间有几个计数点没画出.
将打点计时器接在电压为6V、频率为50Hz的交流电源上,自由下落的重物质量为1kg.如图所示为一条理想的纸带,单位是cm,g取9.8m/s2,O、A之间有几个计数点没画出. 如图所示,水平面上放有10个完全相同的木块(紧靠在一起),每个木块长L=0.6m、质量m=0.5kg,与水平面间的动摩擦因数为μ1=0.1,一个质量M=1kg的铅块(可看作质点)以水平速度v0=5m/s从左端滑上木块,铅块与木块间的动摩擦因数为μ2=0.25,取g=10m/s2,则铅块开始带动木块时的速度为( )
如图所示,水平面上放有10个完全相同的木块(紧靠在一起),每个木块长L=0.6m、质量m=0.5kg,与水平面间的动摩擦因数为μ1=0.1,一个质量M=1kg的铅块(可看作质点)以水平速度v0=5m/s从左端滑上木块,铅块与木块间的动摩擦因数为μ2=0.25,取g=10m/s2,则铅块开始带动木块时的速度为( )