题目内容
9.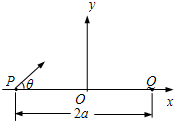 如图所示,平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P点以相同的速率斜向右上方的各个方向射出(即与x轴正方向的夹角θ,0°<θ<90°),经过某一个垂直于xoy平面向里、磁感应强度大小为B的有界匀强磁场区域后,最终会聚到Q点,这些微粒的运动轨迹关于y轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:
如图所示,平面直角坐标系的y轴竖直向上,x轴上的P点与Q点关于坐标原点O对称,距离为2a.有一簇质量为m、带电量为+q的带电微粒,在xoy平面内,从P点以相同的速率斜向右上方的各个方向射出(即与x轴正方向的夹角θ,0°<θ<90°),经过某一个垂直于xoy平面向里、磁感应强度大小为B的有界匀强磁场区域后,最终会聚到Q点,这些微粒的运动轨迹关于y轴对称.为保证微粒的速率保持不变,需要在微粒的运动空间再施加一个匀强电场.重力加速度为g.求:(1)匀强电场场强E的大小和方向;
(2)若微粒在磁场中运动的轨道半径为a,求与x轴正方向成30°角射出的微粒从P点运动到Q点的时间t;
(3)若微粒从P点射出时的速率为v,试推出在x>0的区域中磁场的边界点坐标x与y之间满足的关系式.
分析 (1)离子进入磁场后,电场力下重力合力为0,受到洛伦兹力作用做匀速圆周运动.
(2)先根据几何关系求出进入和离开磁场时的坐标,求出粒子运动的路程,根据时间等于路程除以速率求解;
(3)根据几何关系表示出x、y与半径r的关系,带入数据即可得出x与y之间满足的关系式.
解答 解:(1)由题意可知,微粒所受电场力与重力平衡,即qE=mg
解得:$E=\frac{mg}{q}$,方向竖直向上.
(2)根据题意画出微粒的运动轨迹如图所示,设A、C分别为微粒在磁场中运动的射入点和射出点.根据几何关系可得:
A点坐标为($-\frac{a}{2}$,$\frac{{\sqrt{3}}}{6}a$),C点坐标为($\frac{a}{2}$,$\frac{{\sqrt{3}}}{6}a$)
微粒运动的路程为 $s=\frac{{2\sqrt{3}}}{3}a+\frac{π}{3}a$
设微粒运动的速率为v,它做匀速圆周运动,受到的洛伦兹力提供向心力,即:$Bqv=m\frac{v^2}{r}$
时间:$t=\frac{s}{v}$
解得:$t=\frac{{(2\sqrt{3}+π)m}}{3qB}$
(3)如图所示,设微粒在磁场中运动的轨道半径为r,在x>0的区域内,设微粒离开磁场后的速度方向与x轴夹角为θ.根据几何关系可得:x=rsinθ$y=(\frac{a}{cosθ}-rtanθ)sinθ$
代入相关数据并化简得:$y=\frac{{(ax-{x^2})Bq}}{{\sqrt{{m^2}{v^2}-{B^2}{q^2}{x^2}}}}$
答:(1)匀强电场场强大小是$\frac{mg}{q}$,方向竖直向上
(2)微粒从P点运动到Q点的时间是$\frac{(2\sqrt{3}+π)m}{3qB}$;
(3)微粒在x>0的区域中飞出磁场的位置坐标x与y之间的关系式:$\frac{(ax-{x}^{2})Bq}{\sqrt{{m}^{2}{v}^{2}-{B}^{2}{q}^{2}{x}^{2}}}$
点评 本题是带电粒子在磁场中做匀速圆周运动,要求同学们能画出粒子运动的轨迹,结合几何关系求解,知道半径公式及周期公式,难度较大.

| A. | 登月舱在半径为r2的圆轨道上比在半径为r1的圆轨道上运动时的角速度小 | |
| B. | 登月舱在半径为r2的圆轨道上比在半径为r1的圆轨道上运动时的线速度大 | |
| C. | 月球的质量为$\frac{4{{π}^{2}r}_{1}^{3}}{G{T}_{1}^{2}}$ | |
| D. | 登月舱在半径为r2的圆轨道上运动时的周期为$\sqrt{\frac{{r}_{2}^{2}{T}_{1}^{3}}{{r}_{1}^{2}}}$ |
| A. | 用GPS定位系统研究汽车的运动路线时,可以将汽车看作质点 | |
| B. | 观看跳水运动员的跳水比赛时,可以将运动员看作质点 | |
| C. | 调整人造卫星的姿态使卫星的照相窗口对准地面时,可以将卫星看成质点 | |
| D. | 欣赏运动员的花样滑冰表演时,运动员可以看作质点 |
| A. | 电流 | B. | 电压 | C. | 电荷 | D. | 电阻 |
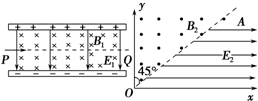 如图所示的平行板之间,存在着相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20T,方向垂直纸面向里,电场强度E1=1.0×105 V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有一边界线AO,与y轴的夹角∠AOy=45°,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,边界线的下方有水平向右的匀强电场,电场强度E2=5.0×105 V/m,在x轴上固定一水平的荧光屏.一束带电荷量q=8.0×10-19 C、质量m=8.0×10-26 kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.4m)的Q点垂直y轴射入磁场区,最后打到水平的荧光屏上的位置C.求:(不计离子的重力影响)
如图所示的平行板之间,存在着相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.20T,方向垂直纸面向里,电场强度E1=1.0×105 V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有一边界线AO,与y轴的夹角∠AOy=45°,边界线的上方有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,边界线的下方有水平向右的匀强电场,电场强度E2=5.0×105 V/m,在x轴上固定一水平的荧光屏.一束带电荷量q=8.0×10-19 C、质量m=8.0×10-26 kg的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.4m)的Q点垂直y轴射入磁场区,最后打到水平的荧光屏上的位置C.求:(不计离子的重力影响) 如图所示,是一个有边界的匀强磁场,磁感应强度B=0.1T,在靠近磁场边缘处放置一个正方形金属线圈abcd,每边长为10cm,每边的等效电阻为0.02Ω,现将线圈沿垂直磁场方向从磁场的右边缘以v=8m/s的速度拉出去,求运动方向上所需要的拉力F多大?(不计重力)
如图所示,是一个有边界的匀强磁场,磁感应强度B=0.1T,在靠近磁场边缘处放置一个正方形金属线圈abcd,每边长为10cm,每边的等效电阻为0.02Ω,现将线圈沿垂直磁场方向从磁场的右边缘以v=8m/s的速度拉出去,求运动方向上所需要的拉力F多大?(不计重力)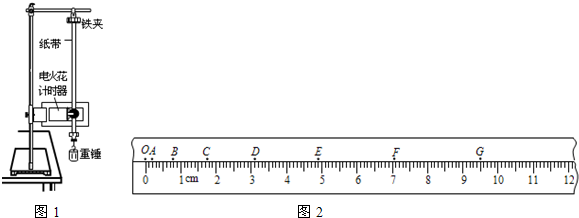
 在“利用单摆测重力加速度”的实验中
在“利用单摆测重力加速度”的实验中