题目内容
5.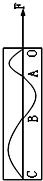 如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求:
如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求:(1)从开始玻璃板从静止下落到运动到画出C点的时间?
(2)玻璃板的加速度?
(3)拉力F为多少?
分析 从固定电动音叉在玻璃上画出的曲线看出OA、AB、BC间对应的时间均为半个周期,玻璃板又做匀加速运动,根据匀变速直线运动的推论△x=aT2求出加速度,再由牛顿第二定律求解外力F的大小.
解答 解:(1)在力F作用下,玻璃板向上作匀加速运动,图示OC间曲线所反映出的是振动的音叉振动位移随时间变化的规律,其中直线OC代表音叉振动1.5个周期内玻璃板运动的位移,而OA、AB、BC间对应的时间均为0.5个周期,即:
t=$\frac{T}{2}=\frac{1}{2f}=\frac{1}{2×5}=0.1s$.
则从O到C的时间为t′=3t=0.3s
(2)设板竖直向上的加速度为a,则有:
sBA-sAO=at2
解得:a=$\frac{0.25-0.15}{0.01}$=10m/s2
(3)由牛顿第二定律得:
F-mg=ma
解得:F=2×(10+10)=40N.
答:(1)从开始玻璃板从静止下落到运动到画出C点的时间为0.3s;
(2)玻璃板的加速度为10m/s2;
(3)拉力F为40N.
点评 本题一要抓住音叉振动与玻璃板运动的同时性,OA、AB、BC对应于音叉振动半个周期.二是利用打点计时器测加速度的原理求解加速度.

练习册系列答案
相关题目
16.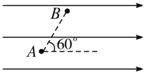 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
 如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )
如图所示,A、B两点相距l=10cm,它们的连线与匀强电场场强方向夹角60°,把电子从A点移到B点,需克服电场力做功3.2×10-18J,则匀强电场的场强等于( )| A. | 800 N/C | B. | 400 N/C | C. | 400$\sqrt{3}$N/C | D. | 800$\sqrt{3}$N/C |
10.汽车以20m/s的速度在平直公路上行驶,遇紧急情况而急刹车获得大小为5m/s2的加速度,则刹车5s后汽车的速度为( )
| A. | 44 m/s | B. | 24 m/s | C. | 4 m/s | D. | 0 |
15.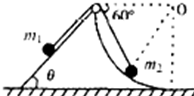 如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
 如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )
如图所示左侧是倾角θ=30°的斜面、右侧是圆弧面的物体固定在水平地面上,圆弧面底端切线水平,一根两端分别系有质量为m1,m2的小球的轻绳跨过其顶点上的小滑轮,当它们处于平衡状态时,连接m2的小球的轻绳与水平线的夹角为60°,不计一切摩擦,两小球可视为质点,两小球的质量之比等于( )| A. | 2:$\sqrt{3}$ | B. | 2:3 | C. | $\sqrt{3}$:2 | D. | 1:1 |
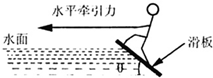 滑板运动是利用汽艇(未画出)牵引运动员在水上滑行的一种运动(如图所示),滑行时汽艇用一根直径为6.3cm,长23cm的拖索拖拉,且拖索头上装有一根直径为25cm~28cm的木质握把供滑水运动员握持.设一个质量为M=70kg的运动员,使用一个质量为m=10kg的滑板滑水,若带动运动员的汽艇以其额定功率P=21kw水平拉着运动员以速度v=108km/h做匀速直线运动,设在运动过程中汽艇受到空气和水的阻力恒为f=100N,水对滑板的作用力垂直于板面,则
滑板运动是利用汽艇(未画出)牵引运动员在水上滑行的一种运动(如图所示),滑行时汽艇用一根直径为6.3cm,长23cm的拖索拖拉,且拖索头上装有一根直径为25cm~28cm的木质握把供滑水运动员握持.设一个质量为M=70kg的运动员,使用一个质量为m=10kg的滑板滑水,若带动运动员的汽艇以其额定功率P=21kw水平拉着运动员以速度v=108km/h做匀速直线运动,设在运动过程中汽艇受到空气和水的阻力恒为f=100N,水对滑板的作用力垂直于板面,则
 在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求
在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求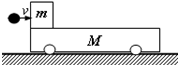 如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求:
如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求: