题目内容
14. 如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求:
如图所示,在光滑水平面上静止着一辆质量为M=10kg的小车,车的上表面水平,小车左端有一质量为m=2kg的物块(可视为质点)处于静止状态,物块和车上表面之间的摩擦因数为μ=0.3,一质量为0.5kg的小球以10m/s的水平速度射向物块,碰撞后以2m/s的速度返回,木块不会从车上掉下来,求:①小车的最大速度.
②小车至少多长,物块才不至于滑落.
分析 小球和木块碰撞过程中,小球和木块组成的系统动量守恒,根据动量守恒定律列式求解木块的速度,当木块和小球速度相等时,两者相对静止,此时速度最大,根据牛顿第二定律求出木块和木板的加速度,再根据运动学基本公式求解小车的最大速度以及小车的最小长度.
解答 解:①小球和木块碰撞过程中,小球和木块组成的系统动量守恒,以小球初速度方向为正,根据动量守恒定律得:
m0v0=mv-m0v′
解得:v=$\frac{0.5×10+0.5×2}{2}$=3m/s
当木块和小车速度相等时,两者相对静止,此时小车速度最大,根据牛顿第二定律得:
木块的加速度a1=$\frac{-μmg}{m}=-0.3×10=-3m/{s}^{2}$,
小车的加速度a2=$\frac{μmg}{M}=\frac{0.3×2×10}{10}=0.6m/{s}^{2}$,
设经过时间t,两者速度相等,则有:
v+a1t=a2t
解得:t=$\frac{3}{3+0.6}=\frac{5}{6}$s
则小车的最大速度vm=a2t=0.6×$\frac{5}{6}$=0.5m/s,
②此过程中,物块运动的位移为:x1=vt+$\frac{1}{2}{a}_{1}{t}^{2}=3×\frac{5}{6}-\frac{1}{2}×3×\frac{25}{36}$=$\frac{35}{24}$m
小车运动的位移为:x2=$\frac{1}{2}{a}_{2}{t}^{2}=\frac{1}{2}×0.6×\frac{25}{36}$=$\frac{5}{24}$m
则小车的长度最少为:x=x1-x2=$\frac{35}{24}$-$\frac{5}{24}$=$\frac{30}{24}$=1.25m
答:①小车的最大速度为0.5m/s.
②小车至少1.25m,物块才不至于滑落.
点评 本题是相对运动的题目,要求同学们能正确分析物体的受力情况和运动情况,根据牛顿第二定律及运动学基本规律解题,难度较大

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案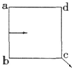 如图所示的正方形区域,在没有磁场的情况下,带电粒子(不计重力)以某一初速度从ab边中点垂直于该边方向射入时,穿过此区域的时间为t1,若在该区域加一垂直纸面向里的匀强磁场,磁感应强度为B,带电粒子仍从同一位置以同一速度入射,粒子从C点射出.若仅B、t为已知量,根据上述条件能求出的物理量为( )
如图所示的正方形区域,在没有磁场的情况下,带电粒子(不计重力)以某一初速度从ab边中点垂直于该边方向射入时,穿过此区域的时间为t1,若在该区域加一垂直纸面向里的匀强磁场,磁感应强度为B,带电粒子仍从同一位置以同一速度入射,粒子从C点射出.若仅B、t为已知量,根据上述条件能求出的物理量为( )| A. | 带电粒子的初速度 | B. | 带电粒子在磁场中运动的半径 | ||
| C. | 带电粒子在磁场中运动的周期 | D. | 带电粒子的质量 |
 如图所示,R3=3Ω,理想电压表读数为2V,理想电流表读数为$\frac{4}{3}$A,某段电路发生故障后,两表的读数变为4.5V和1.5A,求:
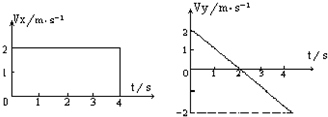
如图所示,R3=3Ω,理想电压表读数为2V,理想电流表读数为$\frac{4}{3}$A,某段电路发生故障后,两表的读数变为4.5V和1.5A,求: 如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求:
如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求: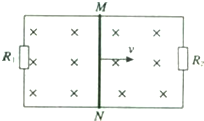 如图所示,在磁感应强度B=0.5T的匀强磁场中,长L=0.4m,电阻r=1.6Ω的导体棒MN在金属框上以v=6m/s的速度向右匀速滑动,其中R1=4Ω,R2=6Ω,其它导线上的电阻不计,求:
如图所示,在磁感应强度B=0.5T的匀强磁场中,长L=0.4m,电阻r=1.6Ω的导体棒MN在金属框上以v=6m/s的速度向右匀速滑动,其中R1=4Ω,R2=6Ω,其它导线上的电阻不计,求: 用一根轻质细绳,一端系住一小球,另一端悬在光滑水平桌面上方高h=0.25m处,绳长大于h,使小球在桌面上做如图所示的匀速圆周运动.重力加速度g=10m/s2,若使小球不离开桌面,其最大转速为( )
用一根轻质细绳,一端系住一小球,另一端悬在光滑水平桌面上方高h=0.25m处,绳长大于h,使小球在桌面上做如图所示的匀速圆周运动.重力加速度g=10m/s2,若使小球不离开桌面,其最大转速为( )