题目内容
17. 在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求
在平面直角坐标系xOy中,第Ⅰ象限存在匀强电场,第Ⅳ象限存在匀强磁场,磁感应强度为B.一质量为m、电荷量为q的带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经x轴上的N点与x轴正方向成θ=60°角射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,如图所示.不计粒子重力,求(1)经过N点的速度v;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t.
分析 (1)粒子垂直于电场进入第一象限,做类平抛运动,根据速度的分解求经过N点的速度v.
(2)粒子由N到达P做匀速圆周运动,由洛伦兹力提供向心力,可由牛顿第二定律求出在磁场中运动的轨道半径r.
(3)根据几何关系求出ON,由类平抛运动的规律求出粒子在电场中运动时间.得到粒子在磁场中转动的圆心角,再由圆周运动的性质求得磁场中运动时间,从而得到总时间.
解答 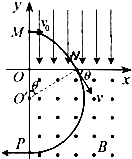 解:(1)设粒子过N点时速度v,有 $\frac{v_0}{v}$=cosθ ①
解:(1)设粒子过N点时速度v,有 $\frac{v_0}{v}$=cosθ ①
可得 v=2v0 ②
(2)粒子在磁场中以O′为圆心做匀速圆周运动,半径为O′N,有
qvB=$\frac{{m{v^2}}}{r}$ ③
得 r=$\frac{{2m{v_0}}}{qB}$ ④
(3)由几何关系得
ON=rsinθ ⑤
粒子在电场中运动的时间t1,有
ON=v0t1 ⑥
可得 t1=$\frac{{\sqrt{3}m}}{qB}$ ⑦
粒子在磁场中做匀速圆周运动的周期
T=$\frac{2πm}{qB}$ ⑧
设粒子在磁场中运动的时间t2,有
t2=$\frac{π-θ}{2π}T$ ⑨
解得 t2=$\frac{2πm}{3qB}$ ⑩
所以总时间为 t=t1+t2
解得 t=$\frac{{(3\sqrt{3}+2π)m}}{3qB}$
答:
(1)经过N点的速度v是2v0;
(2)粒子在磁场中运动的轨道半径r是$\frac{{2m{v_0}}}{qB}$;
(3)粒子从M点运动到P点的总时间t是$\frac{{(3\sqrt{3}+2π)m}}{3qB}$.
点评 粒子在电场中运动偏转时,常运用运动的合成与分解研究.粒子在磁场中做匀速圆周运动的圆心、半径及运动时间的确定也是本题的一个考查重点,要正确画出粒子运动的轨迹图,能熟练运用几何知识解决物理问题.

 快捷英语周周练系列答案
快捷英语周周练系列答案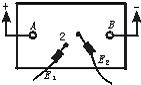 在电场中等势线的描绘实验中所用灵敏电流表的指针偏转方向与电流的关系是:当电流从正接线柱流入电流表G时,指针偏向正接线柱一侧,某同学用这个电表探测基准点2两侧的等势点时,把接电流表正接线柱的E1探针触在基准点2上,把接负接线柱的E2探针接触在纸上某一点,如图所示,若发现电表的指针发生了偏转,该同学移动E2的方向正确的是( )
在电场中等势线的描绘实验中所用灵敏电流表的指针偏转方向与电流的关系是:当电流从正接线柱流入电流表G时,指针偏向正接线柱一侧,某同学用这个电表探测基准点2两侧的等势点时,把接电流表正接线柱的E1探针触在基准点2上,把接负接线柱的E2探针接触在纸上某一点,如图所示,若发现电表的指针发生了偏转,该同学移动E2的方向正确的是( )| A. | 若电表指针偏向正接线柱一侧,E2向右移动 | |
| B. | 若电表指针偏向正接线柱一侧,E2向左移动 | |
| C. | 若电表指针偏向负接线柱一侧,E2向右移动 | |
| D. | 若电表指针偏向负接线柱一侧,E2向左移动 |
| A. | 速度越大,速度变化量不一定越大 | B. | 速度变化越快,加速度就越大 | ||
| C. | 速度越大,速度变化就越快 | D. | 速度变化量越大,速度变化就越快 |
| A. | N | B. | m | C. | m/s | D. | m/s2 |
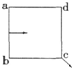 如图所示的正方形区域,在没有磁场的情况下,带电粒子(不计重力)以某一初速度从ab边中点垂直于该边方向射入时,穿过此区域的时间为t1,若在该区域加一垂直纸面向里的匀强磁场,磁感应强度为B,带电粒子仍从同一位置以同一速度入射,粒子从C点射出.若仅B、t为已知量,根据上述条件能求出的物理量为( )
如图所示的正方形区域,在没有磁场的情况下,带电粒子(不计重力)以某一初速度从ab边中点垂直于该边方向射入时,穿过此区域的时间为t1,若在该区域加一垂直纸面向里的匀强磁场,磁感应强度为B,带电粒子仍从同一位置以同一速度入射,粒子从C点射出.若仅B、t为已知量,根据上述条件能求出的物理量为( )| A. | 带电粒子的初速度 | B. | 带电粒子在磁场中运动的半径 | ||
| C. | 带电粒子在磁场中运动的周期 | D. | 带电粒子的质量 |
| A. | “北京时间10点整”,指的是时间间隔,一节课是40min,指的是时刻 | |
| B. | 列车在上海站停了20min,指的是时间间隔 | |
| C. | 1997年7月1日零时中国对香港恢复主权,指的是时间间隔 | |
| D. | “现在是北京时间8点整”,这里实际上指的是时刻 |
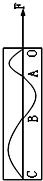 如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求:
如图所示,一块涂有碳黑的玻璃板,质量为2kg,在拉力F的作用下,由静止开始竖直向上做匀变速运动,一个装有水平振针的振动频率为5Hz的固定电动音叉在玻璃板上画出了图示曲线,量得OA=15cm,AB=25,BC=35cm.求: 如图所示,在磁感应强度B=0.5T的匀强磁场中,长L=0.4m,电阻r=1.6Ω的导体棒MN在金属框上以v=6m/s的速度向右匀速滑动,其中R1=4Ω,R2=6Ω,其它导线上的电阻不计,求:
如图所示,在磁感应强度B=0.5T的匀强磁场中,长L=0.4m,电阻r=1.6Ω的导体棒MN在金属框上以v=6m/s的速度向右匀速滑动,其中R1=4Ω,R2=6Ω,其它导线上的电阻不计,求: