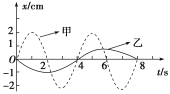
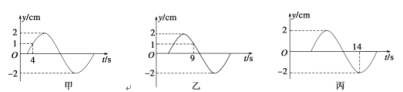
题目内容
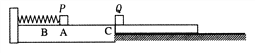
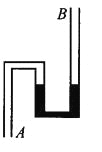
【题目】如图所示,在光滑水平面上有一固定的挡板,挡板左端固定一个轻弹簧。现有一质量M=3kg,长L=4m的小车AB(其中O为小车的中点,OA部分粗糙,OB部分光滑),一质量为m=1kg的小物块(可视为质点)放在车的最左端。车和小物块一起以v0=4m/s的速度在水平面上向右匀速运动,车撞到挡板后瞬间速度变为零,但未与挡板粘连。已知车OB部分的长度大于弹簧的自然长度,弹簧始终处于弹性限度内,小物块与车AO部分之间的动摩擦因数为μ=0.3,重力加速度g=10m/s2。求:
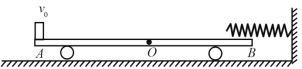
(1)小物块和弹簧相互作用的过程中,弹簧具有的最大弹性势能;
(2)小物块和弹簧相互作用的过程中,弹簧对小物块的冲量;
(3)小物块最终停在小车上的位置距A端多远。
【答案】(1)2J(2)-4kg·m/s(3)1.5m
【解析】
(1)小物块从A到O匀减速直线,由动能定理
-μmg·![]() =
=![]() mv12-mv02
mv12-mv02
小物块压缩弹簧到最短的过程,由能量守恒知
Ep=![]() mv12
mv12
联立解得:
v1=2m/s,Ep=2J
(2)小物块小物块和弹簧相互作用的过程,对小物块由动量定理知
I=-mv1-mv1
解得:
I=-4kg·m/s
冲量大小是4m/s,方向水平向左
(3)小物块相对小车向左滑动的过程,由于
![]() mv12=2J<μmg
mv12=2J<μmg![]() =6J
=6J
因此小物块不会从小车上滑下,最终小物块和小车具有共同速度v共,
选向左为正方向,对小物块和小车组成的系统,
由动量守恒定律知
mv1=(m+M)v共
由能量守恒知
![]() mv12=
mv12=![]() (m+M)v共2+μmgd
(m+M)v共2+μmgd
代入数据解得:
v共=0.5m/s,d=0.5m
小物块最终停在小车上上的位置距A端:
xA=![]() -d=1.5m
-d=1.5m

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目