Question

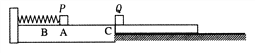
【题目】如图所示，质量为m1=0.5kg的小物块P置于台面上的A点并与弹簧的右端接触(不拴接)，轻弹簧左端固定，且处于原长状态。质量M=l kg的长木板静置于水平面上，其上表面与水平台面相平，且紧靠台面右端。木板左端放有一质量m2=1kg的小滑块Q。现用水平向左的推力将P缓慢推至B点(弹簧仍在弹性限度内)，撤去推力，此后P沿台面滑到边缘C时速度v0=10m／s，与小车左端的滑块Q相碰，最后物块P停在AC的正中点，Q停在木板上。已知台面AB部分光滑，P与台面AC间动摩擦因数μ1=0.1，AC间距离L=4m。Q与木板上表面间的动摩擦因数μ2=0.4，木板下表面与水平面间的动摩擦因数μ3=0.1(g取10m／s2)，求：

(1)撤去推力时弹簧的弹性势能；

(2)长木板运动中的最大速度；

(3)长木板的最小长度。

Answer 1

【答案】（1） 27J （2） 2m/s （3） 3m

【解析】试题分析：研究小物块从P到B再到C的过程，由动能定理列式，可求得弹簧对物块P做的功，从而得到弹簧的弹性势能；小物块P和滑块Q碰撞的过程，遵守动量守恒定律，由此列式．小物块P从碰撞后到静止的过程，由动能定理列式，联立求

出碰后Q获得的速度．Q在木板上滑动时，木板向右加速，Q向右减速，当两者速度相等后一起减速，所以两者共速时Q的速度最大，由牛顿第二定律和速度公式结合求长木板运动中的最大速度；长木板的最小长度等于Q相对于木板的位移大小，由位移公式求解。

（1）小物块从P到B再到C的过程，由动能定理得：

代入数据解得：

根据功能关系知：撤去推力时弹簧的弹性势能为：

（2）小物块P和滑块Q碰撞的过程，取向右为正方向，

由动量守恒定律得：

小物块P从碰撞后到静止的过程，由动能定理得：

代入数据解得：

Q在长木板上滑动的过程中，由牛顿第二定律

对Q：

对木板：

解得：

当物块Q和木板速度相等时，木板的速度最大，设速度为v，滑行时间为t

对Q有：

对木板：

代入数据解得：

所以长木板运动中的最大速度是2m/s．

（3）在Q和木板相对滑动的过程中，Q的位移：

木板的位移：

木板的最小长度：

代入数据解得：