题目内容
【题目】如图所示,质量为3 m的足够长木板C静止在光滑水平面上,质量均为m的两个小物体AB放在C的左端,AB间相距s0,现同时对AB施加水平向右的瞬时冲量而使之分别获得初速度v0和2v0,若AB与C之间的动摩擦因数分别为μ和2μ,则
(1)最终ABC的共同速度为多大?
(2)求运动过程中A的最小速度?
(3)A与B最终相距多远?
(4)整个过程中AB与木板C因摩擦所产生的热量之比为多大?
【答案】(1)0.6v0 (2)vAC=0.5v0 v0=vB
(3)
(4)527
【解析】(1)由于ABC三个物体构成的系统在水平方向不受外力,所以由动量守恒定律可得
mv0+2mv0=5mv
最终ABC的共同速度为
v=0.6v0.
(2)设经t时间A与C恰好相对静止,此时A的速度最小,设为vAC,此时B的速度为vB,由动量守恒和动量定理得
mv0+2mv0=4mvAC+mvB
-μmgt=m(vAC-v0)
(μmg+2μmg)t=3mvAC
解得vAC=0.5v0 vB=v0.
(3)在A与C相对静止前,三个物体的加速度大小分别为aA=
=μg aB=
=2μg aC=
=μg
AB做匀减速运动,C做匀加速运动;在A与C相对静止后,三个物体的加速度大小又分别为
aA′=aC′=
μg aB′=aB=2μg
当AC相对静止后,AC做匀加速运动,B做匀减速运动,最终三个物体以共同速度匀速运动.在开始运动到三个物体均相对静止的过程中AB相对于地面的位移分别为
sA=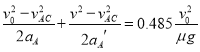
sB=
所以,A与B最终相距
Δs=s0+sB-sA=s0+0.425
(4)设整个运动过程中A相对于C滑行距离为s,则B相对于C滑行的距离为s+Δs-s0,由动能定理得
μmgs+2μmg(s+Δs-s0)=
QA=μmgs
QB=2μmg(s
+Δs-s0)
解得
整个过程中AB与木板C因摩擦所产生的热量之比为
