题目内容
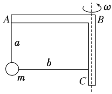
【题目】如图所示,两质量均为m的小球1、2(可视为质点)用一轻质杆相连并置于图示位置,质量也为m的小球3置于水平面OB上,半圆光滑轨道与水平面相切于B点。由于扰动,小球1、2分别沿AO、OB开始运动,当小球1下落h=0.2 m时,杆与竖直墙壁夹角θ=37°,此时小球2刚好与小球3相碰,碰后小球3获得的速度大小是碰前小球2速度大小的![]() ,并且小球3恰好能通过半圆轨道的最高点C,取g=10 m/s2,cos 37°=0.8,sin 37°=0.6,一切摩擦不计,则( )
,并且小球3恰好能通过半圆轨道的最高点C,取g=10 m/s2,cos 37°=0.8,sin 37°=0.6,一切摩擦不计,则( )

A. 小球1在下落过程中机械能守恒
B. 小球2与小球3相碰时,小球1的速度大小为1.6 m/s
C. 小球2与小球3相碰前,小球1的平均速度大于小球2的平均速度
D. 半圆轨道半径大小为R=0.08 m
【答案】D
【解析】
小球1与2连在一起,小球1向下运动的过程中小球2将向右运动,小球1的重力势能减小,小球2的重力势能不变,两个球的动能都增大。由于对1和2球只有重力做功,两个球组成的系统的机械能守恒,但1的机械能不守恒。故A错误;小球1下落h=0.2m时,杆与竖直墙壁夹角θ=37°,将两个小球的速度分解如图: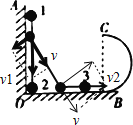
设当小球1下落h=0.2m时小球1的速度是v1,小球2的速度是v2,由图中几何关系,则:v1cos37°=v2sin37°;由机械能守恒得:![]() ;联立得:v1=1.2m/s,v2=1.6m/s。故B错误;设杆的长度为L,由几何关系可得:L-Lcos37°=h,代入数据得:L=1.0m,所以小球2到O点的距离:x2=Lsin37°=1.0×0.6=0.6m;由于两个小球运动的时间相等,而小球2的位移大小大于小球1的位移的大小,所以小球2与小球3相碰前,小球1的平均速度小于小球2的平均速度。故C错误;碰后小球3获得的速度大小是碰前小球2速度的
;联立得:v1=1.2m/s,v2=1.6m/s。故B错误;设杆的长度为L,由几何关系可得:L-Lcos37°=h,代入数据得:L=1.0m,所以小球2到O点的距离:x2=Lsin37°=1.0×0.6=0.6m;由于两个小球运动的时间相等,而小球2的位移大小大于小球1的位移的大小,所以小球2与小球3相碰前,小球1的平均速度小于小球2的平均速度。故C错误;碰后小球3获得的速度大小是碰前小球2速度的![]() ,所以碰撞后小球3的速度:v3=
,所以碰撞后小球3的速度:v3=![]() ×1.6=2m/s;小球3恰好能通过半圆轨道的最高点C,此时的重力提供向心力,所以:
×1.6=2m/s;小球3恰好能通过半圆轨道的最高点C,此时的重力提供向心力,所以:![]() ;小球3从B到C的过程中机械能守恒,则:
;小球3从B到C的过程中机械能守恒,则:![]() ;联立以上方程得:R=0.08m。故D正确。故选D。
;联立以上方程得:R=0.08m。故D正确。故选D。

 备战中考寒假系列答案
备战中考寒假系列答案