题目内容
水平面上两根足够长的光滑金属导轨平行固定放置,间距为L,一端通过导线与阻值R的电阻连接,导轨上放一质量为m的金属杆(见图甲),导轨的电阻忽略不计,匀强磁场方向竖直向下,用与平轨平行的恒定拉力F作用在金属杆上,金属杆从静止开始运动,电压表的读数发生变化,但最终将会保持某一数值U恒定不变;当作用在金属杆上的拉力变为另一个恒定值时,电压表的读数最终相应地会保持另一个恒定值不变,U与F的关系如图乙。若m=0.5kg,L=0.5m,R=0.5Ω,金属杆的电阻r=0.5Ω。(重力加速度g=10m/s2)求:
(1)磁感应强度B;
(2)当F=2.5N时,金属杆最终匀速运动的速度;
(3)在上述(2)情况中,当金属杆匀速运动时,撤去拉力F,此后电阻R上总共产生的热量。
(1)1T (2)10m/s (3)1.25 J
解析:(1)由部分电路欧姆定律![]() ①
①
金属杆所受安培力F安=BIL ②
由于金属杆匀速运动F安=F ③
从U—F图象中取一点F=8N U=8V ④
由①②③④式解得B=1T
(2)当F=2.5N时,由图象可得U=2.5V ⑤
据闭合电路欧姆定律得
![]() ⑥
⑥
金属杆产生的感应电动势
E=BLv ⑦
由⑤⑥⑦式解得: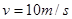
(3)撤去拉力后,金属杆做减速运动,最终静止。
由能量转化守恒定律知电路中产生总的热量
![]() ⑧
⑧
电阻R产生的总热量
![]() ⑨
⑨
由⑧⑨式解得QR=12.5J

 作业辅导系列答案
作业辅导系列答案

 (2013?威海模拟)如图甲所示,水平面上两根足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接.导轨上放一质量为m的金属杆,金属杆、导轨的电阻均忽略不计,匀强磁场垂直导轨平面向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力的大小时,相对应的匀速运动速度v也会变化,v和F的关系如图乙所示.下列说法正确的是( )
(2013?威海模拟)如图甲所示,水平面上两根足够长的金属导轨平行固定放置,间距为L,一端通过导线与阻值为R的电阻连接.导轨上放一质量为m的金属杆,金属杆、导轨的电阻均忽略不计,匀强磁场垂直导轨平面向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力的大小时,相对应的匀速运动速度v也会变化,v和F的关系如图乙所示.下列说法正确的是( ) (2008?滨州一模)水平面上两根足够长的光滑金属导轨平行固定放置,间距为L,一端通过导线与阻值R的电阻连接,导轨上放一质量为m的金属杆(见图甲),导轨的电阻忽略不计,匀强磁场方向竖直向下,用与平轨平行的恒定拉力F作用在金属杆上,金属杆从静止开始运动,电压表的读数发生变化,但最终将会保持某一数值U恒定不变;当作用在金属杆上的拉力变为另一个恒定值时,电压表的读数最终相应地会保持另一个恒定值不变,U与F的关系如图乙.若m=0.5kg,L=0.5m,R=0.5Ω,金属杆的电阻r=0.5Ω.(重力加速度g=10m/s2)求:
(2008?滨州一模)水平面上两根足够长的光滑金属导轨平行固定放置,间距为L,一端通过导线与阻值R的电阻连接,导轨上放一质量为m的金属杆(见图甲),导轨的电阻忽略不计,匀强磁场方向竖直向下,用与平轨平行的恒定拉力F作用在金属杆上,金属杆从静止开始运动,电压表的读数发生变化,但最终将会保持某一数值U恒定不变;当作用在金属杆上的拉力变为另一个恒定值时,电压表的读数最终相应地会保持另一个恒定值不变,U与F的关系如图乙.若m=0.5kg,L=0.5m,R=0.5Ω,金属杆的电阻r=0.5Ω.(重力加速度g=10m/s2)求: