题目内容
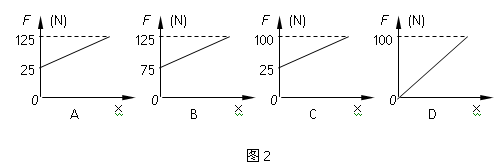
如图1所示,水平面上两根足够长的金属导轨平行固定放置,间距为L=0.5m,一端通过导线与阻值为R为0.5Ω的电阻连接;导轨上放一质量为0.5kg的金属杆,金属杆与导轨的电阻忽略不计;均匀磁场竖直向下.用与导轨平行的恒定拉力F作用在金属杆上,杆最终将做匀速运动.当改变拉力的大小时,相对应的匀速运动速度v也会变化,v与F的关系如图2.则:(g=10m/s2)
(1)金属杆在匀速运动之前做什么运动?
(2)磁感应强度B为多大?
(3)金属杆与导轨间的滑动摩擦因数为多少?

(1)金属杆在匀速运动之前做什么运动?
(2)磁感应强度B为多大?
(3)金属杆与导轨间的滑动摩擦因数为多少?

分析:(1)根据金属杆的受力情况,结合安培力大小与速度成正比,分析在匀速运动之前金属杆的运动情况.
(2)根据安培力表达式F=
和平衡条件,得到v与F的表达式,再结合图象2斜率的意义求解B.
(3)分析图象2截距的意义,求解滑动摩擦因数.
(2)根据安培力表达式F=
| B2L2v |
| R |
(3)分析图象2截距的意义,求解滑动摩擦因数.
解答:解:(1)金属杆在匀速运动之前,水平方向受到拉力F和向左的滑动摩擦力f和安培力FA,由F安=
知,安培力大小与速度大小成正比,开始阶段,拉力大于安培力和滑动摩擦力之和,金属杆做加速运动,随着速度的增大,安培力增大,合力减小,加速度减小,故金属杆在匀速运动之前做变加速直线运动.
(2)杆产生的感应电动势 E=BLv
感应电流 I=
杆所受的安培力 F安=BIL=
当杆匀速运动时,合力为零,则有:F=F安+f
代入得:F=
+f
则得:v=
(F-f)
由图线2得直线的斜率k=2
则得:
=k=2,解得,B=
=
T=1T
(3)由图线2的截距得:f=2
又 f=μmg
则得,μ=
=0.4
答:
(1)金属杆在匀速运动之前做做变加速直线运动.
(2)磁感应强度B为1T.
(3)金属杆与导轨间的滑动摩擦因数为0.4.
| B2L2v |
| R |
(2)杆产生的感应电动势 E=BLv
感应电流 I=
| E |
| R |
杆所受的安培力 F安=BIL=
| B2L2v |
| R |
当杆匀速运动时,合力为零,则有:F=F安+f
代入得:F=
| B2L2v |
| R |
则得:v=
| R |
| B2L2 |
由图线2得直线的斜率k=2
则得:
| R |
| B2L2 |
|
|
(3)由图线2的截距得:f=2
又 f=μmg
则得,μ=
| f |
| mg |
答:
(1)金属杆在匀速运动之前做做变加速直线运动.
(2)磁感应强度B为1T.
(3)金属杆与导轨间的滑动摩擦因数为0.4.
点评:解决本题关键是安培力的分析和计算,根据平衡条件得到F与v的解析式,再分析图象的意义进行求解.对于图象要弄清两坐标轴的物理意义,往往图象的斜率、截距的含义等是解决问题的突破口.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目

 的物体上升。若小车以
的物体上升。若小车以 的速度匀速直线运动,当车后的绳与水平方向的夹角为
的速度匀速直线运动,当车后的绳与水平方向的夹角为 时,物体的速度为
时,物体的速度为 ,绳对物体的拉力为
,绳对物体的拉力为 ,则下列关系式正确的是( )
,则下列关系式正确的是( )
 B.
B.
 D.
D.

 的物体上升。若小车以
的物体上升。若小车以 的速度匀速直线运动,当车后的绳与水平方向的夹角为
的速度匀速直线运动,当车后的绳与水平方向的夹角为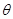 时,物体的速度为
时,物体的速度为 ,绳对物体的拉力为
,绳对物体的拉力为 ,则下列关系式正确的是( )
,则下列关系式正确的是( )



