题目内容
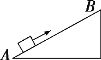
【题目】在水滑的水平面内建立如图所示的直角坐标系，长为L的光滑细杆AB 的两个端点A、B被分别约束在x轴和y轴上运动，现让A沿x轴正方向以速度v0匀速运动，已知P点为杆的中点，杆AB与x轴的夹角为θ。关于P点的运动轨迹和P点的运动速度大小v表达式正确的是( )
A. P点的运动轨迹是一条直线
B. P点的运动轨迹是圆的一部分
C. P点的运动速度大小
D. P点的运动速度大小
【答案】BD
【解析】试题分析：设P点坐标为（x，y），则A、B点的坐标分别为（2x，0）、（0，2y），AB长度一定，设为L，列式求解出x与y的关系式，即为P点的轨迹方程；P点的轨迹是圆，速度是切线方向，画出轨迹图，结合几何关系得到P点速度方向与杆的方向的夹角，P点的速度沿着杆方向的分速度与A点速度沿着杆方向的分速度相等．
设P点坐标为（x，y），则A、B点的坐标分别为（2x，0）、（0，2y），AB长度一定，设为L，根据勾股定理，有： 
，解得
，故P点的运动轨迹是圆，半径为
，故A错误B正确；画出运动轨迹，如图，速度v与杆的夹角
；由于杆子不可以伸长，故P点的速度沿着杆方向的分速度与A点速度沿着杆方向的分速度相等，故
， 
，解得
，故C错误D正确．
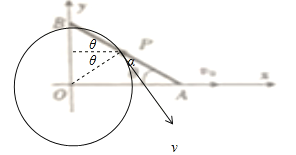
练习册系列答案
相关题目
