题目内容
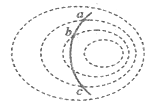
【题目】如图所示，自行车的大齿轮、小齿轮、后轮的半径不一样，它们的边缘有三个点A、B、C。在自行车匀速骑行时，下列说法正确的是
A.A、B两点的角速度大小相等
B.B、C两点的线速度大小相等
C.A点的向心加速度小于B点的向心加速度
D.C点的向心加速度小于B点的向心加速度
【答案】C
【解析】
A.AB两点在传送带上，是同缘传动的边缘点，所以两点的线速度相等，根据v=ωr，由于半径不同，则角速度不相等。故A错误；
B.BC两点属于同轴转动，角速度相等，半径不相等，根据v=rω可知线速度不相等。故B错误；
C.AB两点的线速度相等，根据
，A的半径比较大，所以A点的向心加速度小于B点的向心加速度。故C正确；
D.BC点的角速度是相等的，根据an=ω2r，C点的半径比较大，所以C点的向心加速度大于B点的向心加速度，故D错误；
阅读快车系列答案
【题目】一位同学做“探究弹力大小与弹簧伸长量之间的关系”所测的几组数据如表,请你根据表中数据作出分析。
弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 |
弹簧原来长度L0/cm | 15.0 | 15.0 | 15.0 | 15.0 |
弹簧后来长度L/cm | 16.0 | 17.1 | 17.9 | 19.0 |
弹簧伸长量x/cm | 1.0 | 2.1 | 2.9 | 4.0 |
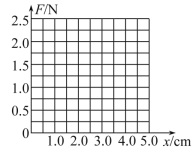
(1)在坐标图上作出F-x图线_______。
(2)写出图线的函数表达式(x用cm作单位):_____________。
(3)函数表达式中常数的物理意义:_________________。
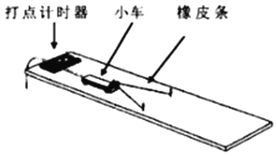
【题目】探究做功与速度变化的关系实验中，某同学利用如图所示的装置，通过数根相同的橡皮条、打点计时器和光滑板面，来探究橡皮条做功与小车获得速度之间的关系。每次改变橡皮条的根数，将小车拉到的光滑板面相同位置由静止释放。得到数据如表所示，则下述说法中正确的是（______）
A | B | C |
橡皮条数 | 速度 | 速度的平方 |
2 | 1.00 | 1.00 |
4 | 1.41 | 1.99 |
6 | 1.73 | 2.99 |
8 | 2.00 | 4.00 |
A．利用改变橡皮条的根数来改变做功的大小，使做功数值倍数增加
B．改变橡皮条的根数重新做的这4次实验，必须不断改变板面与水平面的倾角
C．从表格A列和B列对比，可以判断在误差允许范围内，橡皮条做功与小车速度成正比例关系
D．从表格A列和C列对比，可以判断在误差允许范围内，橡皮条做功与小车速度平方成正比例关系
