题目内容
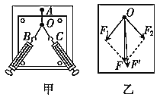
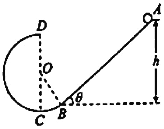
【题目】如图所示,竖直平面内有一固定的光滑轨道ABCD,其中倾角θ=37°的斜面AB与半径为R的圆弧轨道平滑相切于B点,CD为竖直直径,O为圆心,质量为m的小球(可视为质点)从与B点高度差为h的斜面上的A点处由静止释放,重力加速度大小为g,sin37°=0.6,cos37°=0.8,则下列说法正确的是
A. 当h=3R时,小球过C点时对轨道的压力大小为![]()
B. 当h=2R时,小球会从D点离开圆弧轨道作平抛运动
C. 调整h的值,小球能从D点离开圆弧轨道,并能恰好落在B点
D. 调整h的值,小球能从D点离开圆弧轨道,但一定不能落在B点
【答案】D
【解析】
A.当h=3R时,小球从A点到C点的过程,根据机械能守恒有:
![]()
小球过C点时有:
![]()
联立解得:
FN=7.4mg
据牛顿第三定律可知,小球过C点压力大小为7.4mg,故A错误;
B.若小球恰好从D点离开圆弧轨道,则有:
![]() ,
,
从开始到D的过程,有
mg(h0-R-Rcosθ)=![]() mv02
mv02
解得:
![]() ,
,
h0=2.3R>2R
所以当h=2R时,小球在运动到D前已经脱离轨道,不会从D点离开做平抛运动,故B错误;
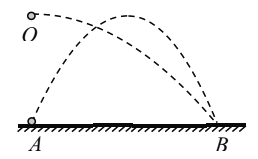
CD.若小球以速度v0从D点离开后做平抛运动,则
R+Rcosθ=![]() gt2
gt2
得:
![]()
且
![]()
所以小球能从D点离开圆弧轨道,但一定不能落在B点,故D正确,C错误。

练习册系列答案
相关题目