题目内容
【题目】如图所示，水平面上固定着不等间距的两段平行直导轨，处于磁感应强度大小为B的竖直向下的匀强磁场中，粗糙导轨PQ、P'Q'的宽度私L,光滑导轨MN、M'N'无限长，其宽度为2L,导轨电阻均不计金属棒ab、cd垂直放置于两段导轨上与导轨接触良好，均可自由滑动，其质量分别为m和2m,二者接入电路的电阻分别为R和2R，一根轻质细线绕过定滑轮(定滑轮用绝缘材料固定在轨道平面内，滑轮质量和摩擦不计)，一端系在金属棒ab的中点上，另一端悬挂一物块W,W的质量着M，此时金属棒ab恰好不滑动。现用水平向右的恒定拉F使金属棒cd由静止开始向右运动，当cd达到最大速度时金属棒ab即将滑动，已知重力加速度g求：
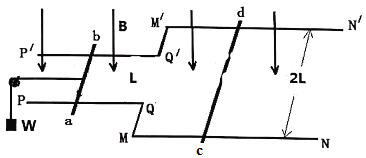
(1)金属棒cd的最大速度vm
(2)恒定拉力F的大小
(3)若在金属棒cd达到最大速度时立即撤去拉力F,试计算出金属棒cd继续运动的位移S
(4)若金属棒cd从静止开始运动到达到最大速度所用时间为t,则金属棒ab从棒cd开始运动到静止共产生了多少焦耳热？
【答案】（1）
（2）
（3）
（4）
【解析】
考查力的平衡、动量定理、动能定理的综合应用，根据相关规律计算可得。
当
棒达到最大速度
时，
棒恰好未发生相对滑动，对棒受力分析可得
受拉力
作用前，由平衡条件：
解得
对棒：
解得：
当棒达到最大速度时，此时受力平衡，则外力
又：
故：
（3）金属棒达到最大速度时立即撤去拉力，直至停止，对棒应用动量定理：
又：
故：
联立解得继续运动的位移
（4）导体棒加速过程中，对棒应用动量定理：
联立可得加速过程的位移：
设棒克服安培力做功为
，对棒运动全过程应用动能定理：
，
设系统产生焦耳热为
，由能的转化与守恒定律可知：
解得
练习册系列答案
提分百分百检测卷系列答案
相关题目
