题目内容
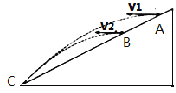
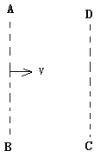
【题目】在折射率为n，厚度为d的玻璃平板上方的空气中有一点光源S，从S发出的光线SA以入射角θ 入射到玻璃板上表面，经过玻璃板后从下表面射出，如图所示。若沿此光线传播的光从光源 S 到玻璃板上表面的传播时间与在玻璃板中传播时间相等，点光源S到玻璃板上表面的垂直距离l应是多少？
【答案】
【解析】
设光线SA在玻璃中的折射角为θ2，传播速度为v，则由
有，光在玻璃板中传播的速度
；由几何关系有，光线在玻璃板上表面传播的距离为
，由s＝vt，有
＝
，其中c是真空中的光速，光在玻璃板中传播的距离
，光在玻璃板中的传播时间
＝
由折射定律有：
①
由题意有：＝②
由三角函数关系有：cos θ2＝
③
联立①②③得：l＝
思路根据几何知识以及直线运动规律算出在玻璃板上表面传播的时间，在算出光在玻璃板中传播的时间，根据折射定律，联立等式可解题
练习册系列答案
相关题目
【题目】一实验小组准备探究某合金材料制成的电子元件Z的伏安特性曲线,他们连接了如图所示的实物图。
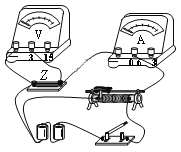
(1)我们通常把电压表和电流表的读数当做元件Z上电压和电流的测量值。若考虑电表内阻的影响,该元件电压的测量值__________真实值,电流的测量值__________真实值(选填“大于”、“等于”或“小于”)。
(2)实验测得表格中的9组数据,请在图中的坐标纸上作出该元件的伏安特性图线。
序号 | I/A | U/V |
1 | 0 | 0 |
2 | 0.06 | 0.12 |
3 | 0.08 | 0.20 |
4 | 0.12 | 0.42 |
5 | 0.16 | 0.80 |
6 | 0.20 | 1.24 |
7 | 0.24 | 1.80 |
8 | 0.26 | 2.16 |
9 | 0.30 | 2.80 |
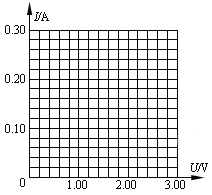
(3)元件Z在U=0.80V时的电阻值是__________Ω(保留两位有效数字),图线在该点的切线斜率的倒数__________电阻值(选填“大于”、“等于”或“小于”)。
