题目内容
11.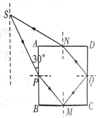 一立方体透明物体横截面如图所示,底面BC和右侧面CD均镀银(图中粗线),P、M、Q、N分别为AB边、BC边、CD边、AD边的中点,左端的竖直虚线在ABCD所在的平面内并与AB平行,虚线上有一点光源S,从S发出一条细光线射到P点时与PA的夹角成30°,经折射后直接射到M点,从透明物体的AD面上射出后刚好可以回到S点.试求:(为计算简便,sin15°取0.25,结果可用根式表示)
一立方体透明物体横截面如图所示,底面BC和右侧面CD均镀银(图中粗线),P、M、Q、N分别为AB边、BC边、CD边、AD边的中点,左端的竖直虚线在ABCD所在的平面内并与AB平行,虚线上有一点光源S,从S发出一条细光线射到P点时与PA的夹角成30°,经折射后直接射到M点,从透明物体的AD面上射出后刚好可以回到S点.试求:(为计算简便,sin15°取0.25,结果可用根式表示)(1)透明物体的折射率n;
(2)若光在真空中的速度为c,正方形ABCD的边长为a,则光从S点发出后,经过多长时间射回S点?
分析 (1)根据几何关系求出光线在P点折射时的入射角和折射角,再根据光的折射定律即可求解折射率;
(2)根据几何知识求出光线在正方形ABCD内传播的距离,由v=$\frac{c}{n}$求出光在正方形ABCD中的传播速度,再求在正方体中传播的时间.再加上在正方体外传播的时间即为所求.
解答 解:(1)根据题意作光路图,光线在P点发生折射时,入射角为 i=60°,折射角为 r=45°
因此透明物体的折射率 n=$\frac{sini}{sinr}$=$\frac{sin60°}{sin45°}$=$\frac{\sqrt{6}}{2}$
(2)连接PN,由几何关系可得,PN,PM,QN,QM的长均为$\frac{\sqrt{2}}{2}$a,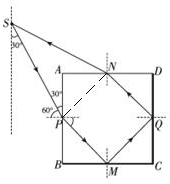
且∠PSN=30°,SN=SP=$\frac{\frac{\sqrt{2}}{4}}{sin15°}$=$\sqrt{2}$a
光在透明物体中的速度 v=$\frac{c}{n}$
光透明物体中传播所用的时间 t1=$\frac{PM+QM+QN}{v}$;
光在透明物体外传播所用的时间 t2=$\frac{SP+SN}{c}$
那么光从S点发出射回到S点所经历的总时间为 t=t1+t2.
联立解得 t=$\frac{(4\sqrt{2}+3\sqrt{3})a}{2c}$
答:(1)透明物体的折射率是$\frac{\sqrt{6}}{2}$;
(2)光从S点发出后,经过$\frac{(4\sqrt{2}+3\sqrt{3})a}{2c}$时间射回S点.
点评 本题光的折射定律和光速公式的应用问题,关键要运用几何知识求光线传播的距离,掌握传播速度与折射率的关系,注意要画出正确的光路图.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2.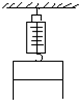 如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
 如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )
如图所示,封有空气的气缸挂在测力计上,测力计的示数为F,且已知气缸套的质量为M,活塞的质量为m、面积为S,气缸壁与活塞间摩擦不计,外界大气压强为p0,则气缸内空气的压强为( )| A. | p0-$\frac{Mg}{s}$ | B. | p0+$\frac{(Mg-F)}{S}$ | C. | p0-$\frac{[F-(m+M)g]}{S}$ | D. | p0-$\frac{mg}{s}$ |
6.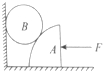 如图所示,截面为$\frac{1}{4}$圆周的柱状物体A放在光滑水平地面上,A与墙面之间放一光滑的圆柱形物体B,在水平向左的力F的作用下系统处于静止状态,现使A向右移动少许(B未落地),在F的作用下系统仍处于静止状态.则( )
如图所示,截面为$\frac{1}{4}$圆周的柱状物体A放在光滑水平地面上,A与墙面之间放一光滑的圆柱形物体B,在水平向左的力F的作用下系统处于静止状态,现使A向右移动少许(B未落地),在F的作用下系统仍处于静止状态.则( )
 如图所示,截面为$\frac{1}{4}$圆周的柱状物体A放在光滑水平地面上,A与墙面之间放一光滑的圆柱形物体B,在水平向左的力F的作用下系统处于静止状态,现使A向右移动少许(B未落地),在F的作用下系统仍处于静止状态.则( )
如图所示,截面为$\frac{1}{4}$圆周的柱状物体A放在光滑水平地面上,A与墙面之间放一光滑的圆柱形物体B,在水平向左的力F的作用下系统处于静止状态,现使A向右移动少许(B未落地),在F的作用下系统仍处于静止状态.则( )| A. | 水平外力F增大 | B. | 墙对B的作用力减小 | ||
| C. | 地面对A的支持力减小 | D. | B对A的作用力减小 |
16.把阻值为5Ω、5Ω、10Ω的三个电阻任意连接,得到的等效电阻的阻值( )
| A. | 在5Ω到10Ω之间 | B. | 在2Ω到10Ω之间 | C. | 小于2Ω | D. | 大于20Ω |
1.下列对关系式Uab=Ed的理解,错误的是( )
| A. | 式中的d是a,b两点间的距离 | B. | a,b两点间距离越大,电势差越大 | ||
| C. | d是a,b两个等势面的垂直距离 | D. | 此式适用于任何电场 |
 质量m=1kg的物体,在水平拉力F(拉力方向与物体初速度方向相同)的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止,运动过程中Ek-x的图线如图所示.求:(g取10m/s2)
质量m=1kg的物体,在水平拉力F(拉力方向与物体初速度方向相同)的作用下,沿粗糙水平面运动,经过位移4m时,拉力F停止作用,运动到位移是8m时物体停止,运动过程中Ek-x的图线如图所示.求:(g取10m/s2)