题目内容
【题目】如图所示为直角三角形斜劈ABC,∠ABC=60°,P为AB的中点,AP=PB=10m。小物块与AP段的动摩擦因数为μ1,与PB段的动摩擦因数为μ2。第一次将BC水平放置,小物块从A点静止释放,滑到B点时速度刚好为零。第二次将AC水平放置,g取10m/s2,下列说法正确的是
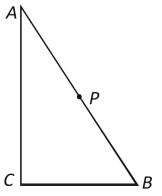
A. 第一次下滑过程中小物块经过AP段和PB段的时间之比为1︰(![]() -1)
-1)
B. μ1+μ2=2![]()
C. 若第二次小物块在B点由静止释放则一定不下滑
D. 若第二次在B点给小物块一个初速度v0=15m/s,小物块刚好能滑到最底端A点
【答案】BC
【解析】
第一次物体先加速后减速到零,根据两段的平均速度判断时间关系;在整个过程中由动能定理可求解两动摩擦因数的关系;根据在斜面上时的重力沿斜面向下的分力与摩擦力的关系判断物体能否下滑;假设物体能到达斜面最低点,根据动能定理列出方程求解最低点的速度,从而进行判断.
第一次下滑过程中,因初速度为零,末速度为零,则物体一定是先加速后减速,若设到达P点的速度为v,则AP和BP两段的平均速度均为v/2,则小物块经过AP段和PB段的时间之比为1:1,选项A错误;设AB=2L,从A到B由动能定理:![]() ,解得μ1+μ2=2
,解得μ1+μ2=2![]() ,选项B正确;
,选项B正确;
第一次从A开始时下滑时满足![]() ,即
,即 ![]() ;则
;则![]() ;第二次小物块在B点由静止释放,则
;第二次小物块在B点由静止释放,则![]() 成立,则小物块在B点由静止释放则一定不下滑,选项C正确;若第二次在B点给小物块一个初速度v0=15m/s,设小物块滑到最底端A点的速度为v′,则由动能定理:
成立,则小物块在B点由静止释放则一定不下滑,选项C正确;若第二次在B点给小物块一个初速度v0=15m/s,设小物块滑到最底端A点的速度为v′,则由动能定理:![]() ,解得v′2=-175可知,物块不能到达A点,选项D错误;故选BC.
,解得v′2=-175可知,物块不能到达A点,选项D错误;故选BC.

 七星图书口算速算天天练系列答案
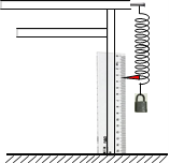
七星图书口算速算天天练系列答案【题目】某同学在实验室做“探究弹簧弹力的大小与伸长量的关系”实验时,将弹簧悬挂在铁架台上,将刻度尺竖直固定在弹簧一侧,刻度尺的零刻度线刚好与弹簧上端相齐,读出此时弹簧的长度![]() =25.35cm。在弹簧下端悬挂1个钩码时,弹簧的长度为L1;每次增加1个钩码,分别读出弹簧长度为L2、L3……。已知单个钩码的质量为m=50g,重力加速度g=9.8N/kg。
=25.35cm。在弹簧下端悬挂1个钩码时,弹簧的长度为L1;每次增加1个钩码,分别读出弹簧长度为L2、L3……。已知单个钩码的质量为m=50g,重力加速度g=9.8N/kg。
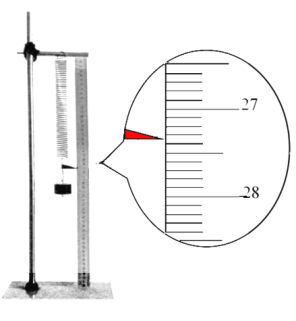
(1)L1的读数如图所示,将L1的数值填入下表__________。
代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
数值/cm | 25.35 |
| 29.35 | 31.30 | 33.40 | 35.35 | 37.40 | 39.35 |
(2)该同学根据表中的数据做出m-L图像,如图所示。其中图像横轴代表弹簧的长度,纵轴代表所悬挂钩码的质量。除第2组数据外,其它数据已在坐标系中描绘出对应点。请将第2组数据的对应点标记在相应位置,并绘出m-L图像__________。
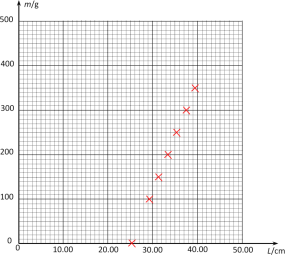
(3)由图像可知,该弹簧的劲度系数k=__________N/m(结果保留两位小数)。
(4)另一同学在家测弹簧的劲度系数。他将弹簧挂在桌子的边缘,如图所示,找到了质量为m的3个同样的铁锁和一把刻度尺,实验时,他将刻度尺竖直立在桌腿边缘靠近弹簧的位置。当挂1个铁锁时,弹簧的指针指在l1位置;当挂3个铁锁时,弹簧的指针指在l2位置。重力加速度为g。由此可得该弹簧的劲度系数k=________(用l1、l2、m、g表示)。