题目内容
9.在图(a)所示的电路中,电阻值均为R,则A、B两点之间的等效电阻RAB=$\frac{7}{12}$R.在图(b)所示的有限网络中,每一小段导体的电阻值均为R,则A、B两点之间的等效电阻RAB=$\frac{6}{11}$R.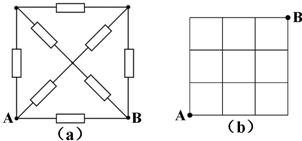
分析 (a)画出AB间的等效电路,利用串并联电路知识和欧姆定律求电阻;
(b)垂直于AB做直线,AB的垂直平分线的四个点电势相等,可以直接短路,利用串并联电路知识和欧姆定律求电阻.
解答 解:(a)电阻编号如图所示: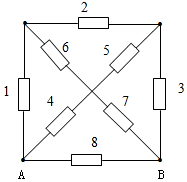
AB间等效电路为: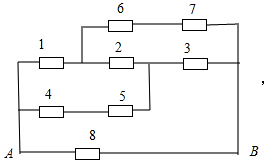
设电源电压为U,干路电流为I,则等效电阻为:R等=$\frac{U}{I}$,对1、2、3、4、5、6、7组成的部分,设靠近A端的电阻R两端的电压为kU(0<k<1为待定系数),则靠近B端的电阻R两端的电压也为kU,则两电阻2R两端的电压都为(1-k)U,中间电阻2两端的电压应为(1-2k)U,
考虑节点电流,流入电流等于流出电流,则有:
(1-k)$\frac{U}{2R}$+(1-2k)$\frac{U}{R}$=k$\frac{U}{R}$
解得:k=$\frac{3}{7}$
则总电流为:I=k$\frac{U}{R}$+(1-k)$\frac{U}{2R}$
代入k=$\frac{3}{7}$,可得:I=$\frac{5U}{7R}$,代入R等=$\frac{U}{I}$得:
R等=$\frac{7}{5}$R,
故可知AB等效电阻为:$\frac{1}{{R}_{AB}}$=$\frac{1}{\frac{7}{5}R}$+$\frac{1}{R}$
解得:RAB=$\frac{7}{12}$R
(b)垂直于AB做直线,AB的垂直平分线的四个点电势相等,可以直接短路;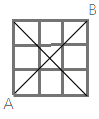
可以AB间等效电阻为:$\frac{1}{{R}_{AB}}$=$\frac{R}{2}$+$\frac{R}{4}$+$\frac{R}{6}$+$\frac{R}{6}$+$\frac{R}{4}$+$\frac{R}{2}$
解得:RAB=$\frac{6}{11}$R
故答案为:$\frac{7}{12}$R;$\frac{6}{11}$R.
点评 该题先要会画等效电路,能掌握节点电流法是解题关键,结合串并联电路知识解决.

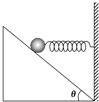 如图为一位于墙角的斜面,其倾角为37°,一轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球在斜面上静止时,弹簧处于伸长状态,则( )
如图为一位于墙角的斜面,其倾角为37°,一轻质弹簧一端系在质量为m的小球上,另一端固定在墙上,弹簧水平放置,小球在斜面上静止时,弹簧处于伸长状态,则( )| A. | 小球一定受四个力作用 | |
| B. | 弹簧弹力可能是$\frac{4}{3}mg$ | |
| C. | 小球受木板的摩擦力一定沿斜面向上 | |
| D. | 斜面对小球的作用力方向一定竖直向上 |
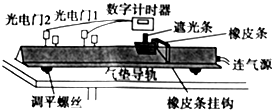
| A. | 时间间隔 | B. | 位移 | C. | 平均速度 | D. | 瞬时速度 |
| A. | 气体对容器的压强是大量气体分子对容器的碰撞引起的,它跟气体的重力无关 | |
| B. | 用气筒给自行车打气,越压缩越费劲,这是因为气体分子之间斥力变大 | |
| C. | 由于液体分子的热运动,液体会表现出各向同性 | |
| D. | 非晶体的微观结构跟液体非常相似,非晶体会表现出各向同性 | |
| E. | 由于多晶体是由许多单晶体杂乱无章地组合而成,所以多晶体各向异性 |
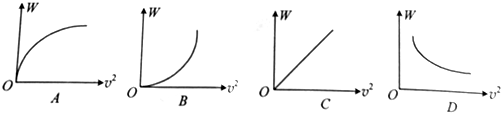
| A. | 单摆做简谐振动,振幅越大,周期越大 | |
| B. | 水面上的油膜呈现彩色是光的干涉现象 | |
| C. | 在光电效应实验中,用同种频率的光照射不同的金属表面,从金属表面逸出的光电子,最大初动能Ek越大,则这种金属的逸出功W0越小 | |
| D. | 比结合能越大,原子核中核子结合得越牢固,原子核越稳定 |

 如图所示,把质量是3kg的石块从高为10m的山崖上向斜上方抛出,抛出的初速度大小为5m/s,若不计空气阻力,g取10m/s2,求石块落地时的速度大小.
如图所示,把质量是3kg的石块从高为10m的山崖上向斜上方抛出,抛出的初速度大小为5m/s,若不计空气阻力,g取10m/s2,求石块落地时的速度大小.