题目内容
1.一物体沿直线运动时,它的速度图象如图所示,由图可知( )
| A. | 1s末物体返回出发点 | |
| B. | 2s末物体运动方向改变 | |
| C. | 前3s内物体位移为1m | |
| D. | 第2s内和第4s内物体加速度大小相等 |
分析 v-t图象中,倾斜的直线表示匀变速直线运动,斜率表示加速度,倾斜角越大表示加速度越大,图象与坐标轴围成的面积表示位移.由此分析.
解答 解:A、1s末物体的速度为0,位移不为0,物体没有返回出发点,故A错误;
B、由图象可知1至3s末,速度图象都在时间轴的上方,都大于零,方向一直没有改变,故B错误;
C、图象与坐标轴围成的面积表示位移,前3s的位移等于第3s内的位移,为:s=$\frac{1}{2}$×1×2m=1m,故C正确;
D、v-t图象的斜率表示加速度,由图可知第2s内和第4s内物体加速度大小,方向相反,故D正确.
故选:CD
点评 本题是为速度--时间图象的应用,要明确斜率的含义,知道在速度--时间图象中图象与坐标轴围成的面积的含义,能根据图象读取有用信息.

练习册系列答案
相关题目
17.在物理学发展的过程中,有许多伟大的科学家做出了突出贡献,关于科学家和他们的贡献,下列说法正确的是( )
| A. | 伽利略通过“理想实验”得出结论:运动必具有一定速度,如果它不受力,它将以这一速度永远运动下去 | |
| B. | 德国天文学家开普勒对他导师第谷观测的行星数据进行多年研究,得出了万有引力定律 | |
| C. | 牛顿发现了万有引力定律,卡文迪许通过实验测出了引力常量 | |
| D. | 古希腊学者亚里士多德认为物体下落快慢由它们的重量决定,牛顿利用逻辑推断使亚里士多德的理论陷入了困境 |
12.物体在一对平衡力作用下,处于静止状态,今保持其中一个力不变而将另一个力先逐渐减小为零,再逐渐恢复到原来的大小,则在这段时间内( )
| A. | 物体的动量先增大后减小 | |
| B. | 物体的动量一直增大 | |
| C. | 当变化的力减为零时,物体的动量变化最大 | |
| D. | 当两个力再次平衡时,物体的动量变化最大 |
9. 如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
 如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )
如图所示,在水平地面上叠放着A、B、C三个完全相同的物块,今用水平力F作用于B时,A、B、C均处于静止状态,则不正确的是( )| A. | 地面对C的摩擦力等于F | B. | A对B的摩擦力等于$\frac{F}{2}$ | ||
| C. | B对A的摩擦力等于零 | D. | B对C的摩擦力等于F方向向右 |
16. 如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2).
如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2).
 如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2).
如图所示,物体质量为1kg,斜向上的拉力F=10N,物体和水平面间的动摩擦因数μ=0.5,物体在F的作用下由静止开始运动10s,则在这段时间内拉力F对物体做功为2400J (g取10m/s2).
6. 如图所示,重物重力为G,轻绳AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,则AO段的拉力F1、BO段的拉力F2和物体的重力大小间的关系正确的是( )
如图所示,重物重力为G,轻绳AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,则AO段的拉力F1、BO段的拉力F2和物体的重力大小间的关系正确的是( )
 如图所示,重物重力为G,轻绳AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,则AO段的拉力F1、BO段的拉力F2和物体的重力大小间的关系正确的是( )
如图所示,重物重力为G,轻绳AO和BO的A、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,则AO段的拉力F1、BO段的拉力F2和物体的重力大小间的关系正确的是( )| A. | F12+G2=F22 | B. | F1=Gtgθ | C. | F2=F1cosθ | D. | F2=Gsinθ |
13.一般教室门上都安装一种暗锁,这种暗锁由外壳A、骨架B、弹簧C(劲度系数为k)、锁舌D(倾斜角θ=45°)、锁槽E,以及连杆、锁头等部件组成,如图1所示.设锁舌D与外壳A和锁槽E之间的摩擦因数均为μ且受到的最大静摩擦力 f=μN(N为正压力).有一次放学后,当某同学准备锁门时,他加最大力时,也不能将门关上(由于摩擦因数增大,此种现象称为自锁),此刻暗锁所处的状态如图2所示,P为锁舌D与锁槽E之间的接触点,弹簧由于被压缩而缩短了x.则( )


| A. | 锁舌D与锁槽E之间的正压力的大小为$\frac{\sqrt{2}kx}{1-2μ-{μ}^{2}}$ | |
| B. | 锁舌D与锁槽E之间的正压力的大小$\frac{kx}{1-2{μ}^{2}}$ | |
| C. | 出现自锁现象的最小摩擦因数为μ=0.414 | |
| D. | 出现自锁现象的最小摩擦因数为μ=0.207 |
10.关于矢量和标量,下列说法中正确的是( )
| A. | 位移、速度、质量是矢量,时间、加速度、长度是标量 | |
| B. | 时间、位移、速度是矢量,加速度、长度、质量是标量 | |
| C. | 加速度、位移、速度是矢量,时间、质量、长度是标量 | |
| D. | 长度、速度、质量是矢量,位移、时间、加速度是标量 |
11.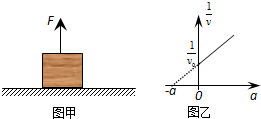 如图甲所示,静止在水平面上的物体在竖直向上的拉力F作用下开始向上加速运动,拉力的功率恒定为P,运动过程中所受空气阻力大小不变,物体最终做匀速运动.物体运动速度的倒数与加速度a的关系如图乙所示.若重力加速度大小为g,下列说法正确的是( )
如图甲所示,静止在水平面上的物体在竖直向上的拉力F作用下开始向上加速运动,拉力的功率恒定为P,运动过程中所受空气阻力大小不变,物体最终做匀速运动.物体运动速度的倒数与加速度a的关系如图乙所示.若重力加速度大小为g,下列说法正确的是( )
 如图甲所示,静止在水平面上的物体在竖直向上的拉力F作用下开始向上加速运动,拉力的功率恒定为P,运动过程中所受空气阻力大小不变,物体最终做匀速运动.物体运动速度的倒数与加速度a的关系如图乙所示.若重力加速度大小为g,下列说法正确的是( )
如图甲所示,静止在水平面上的物体在竖直向上的拉力F作用下开始向上加速运动,拉力的功率恒定为P,运动过程中所受空气阻力大小不变,物体最终做匀速运动.物体运动速度的倒数与加速度a的关系如图乙所示.若重力加速度大小为g,下列说法正确的是( )| A. | 物体的质量为$\frac{P}{v{{\;}_{0}a}_{0}}$ | B. | 空气阻力大小为$\frac{P({a}_{0}-g)}{v{{\;}_{0}a}_{0}}$ | ||
| C. | 物体加速运动的时间为$\frac{{v}_{0}}{{a}_{0}}$ | D. | 物体匀速运动的速度大小为v0 |