题目内容
6.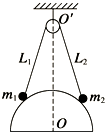 表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )
表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )| A. | $\frac{{m}_{1}}{{m}_{2}}$=$\frac{24}{25}$ | B. | $\frac{{m}_{1}}{{m}_{2}}$=$\frac{25}{24}$ | C. | $\frac{{N}_{1}}{{N}_{2}}$=$\frac{25}{24}$ | D. | $\frac{{N}_{1}}{{N}_{2}}$=$\frac{24}{25}$ |
分析 分别以两个小球为研究对象,分析受力情况,作出力图,运用三角形相似法得出绳子拉力、支持力与重力的关系式,再求解质量之比和压力之比.
解答  解:先以左侧小球为研究对象,分析受力情况:重力m1g、绳子的拉力T和半球的支持力N,作出力图.
解:先以左侧小球为研究对象,分析受力情况:重力m1g、绳子的拉力T和半球的支持力N,作出力图.
由平衡条件得知,拉力T和支持力N的合力与重力mg大小相等、方向相反.设OO′=h,根据三角形相似得:
$\frac{T}{{L}_{1}}=\frac{{m}_{1}g}{h}$=$\frac{{N}_{1}}{R}$,
同理,对右侧小球,有:
$\frac{T}{{L}_{2}}=\frac{{m}_{2}g}{h}$=$\frac{{N}_{2}}{R}$,
解得:
m1g=$\frac{Th}{{L}_{1}}$…①
m2g=$\frac{Th}{{L}_{2}}$…②
N1=$\frac{{{m_1}gR}}{h}$…③
N2=$\frac{{{m_2}gR}}{h}$…④
由①:②得
m1:m2=L2:L1=25:24,
由③:④得
N1:N2=m1:m2=L2:L1=25:24,
故AD错误,BC正确;
故选:BC.
点评 本题运用三角形相似法处理非直角三角形的力平衡问题,抓住两球所受的绳子拉力相等是桥梁.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
16.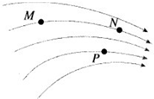 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点,下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点,下列判断正确的是( )
 如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点,下列判断正确的是( )
如图为某一电场的电场线,M、N、P为电场线上的三个点,M、N是同一电场线上两点,下列判断正确的是( )| A. | M、N、P三点中N点的场强最大 | |
| B. | M、N、P三点中N点的电势最高 | |
| C. | 负电荷在M点的电势能大于在N点的电势能 | |
| D. | 正电荷从M点自由释放,电荷将沿电场线运动到N点 |
14.关于速度和速率,下列说法正确的是( )
| A. | 物体有恒定的速率时,速度不可能变化 | |
| B. | 物体有恒定的速度时,其速率仍可能有变化 | |
| C. | 瞬时速度是指物体经过某一时刻(或某一位置)的速度,它的大小简称速率 | |
| D. | 物体运动速度发生变化时,一定是速度大小发生了变化 |
1.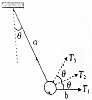 如图所示,用竖直方向成θ角(θ<45°)的轻绳a和b共同固定一个小球,当绳b水平时,拉力为T1,现保持小球在原位置不动,使绳b在竖直平面内从水平方向逆时针转过θ角固定,绳b的拉力变为T2;再转过θ角固定,绳b的拉力为T3,则( )
如图所示,用竖直方向成θ角(θ<45°)的轻绳a和b共同固定一个小球,当绳b水平时,拉力为T1,现保持小球在原位置不动,使绳b在竖直平面内从水平方向逆时针转过θ角固定,绳b的拉力变为T2;再转过θ角固定,绳b的拉力为T3,则( )
 如图所示,用竖直方向成θ角(θ<45°)的轻绳a和b共同固定一个小球,当绳b水平时,拉力为T1,现保持小球在原位置不动,使绳b在竖直平面内从水平方向逆时针转过θ角固定,绳b的拉力变为T2;再转过θ角固定,绳b的拉力为T3,则( )
如图所示,用竖直方向成θ角(θ<45°)的轻绳a和b共同固定一个小球,当绳b水平时,拉力为T1,现保持小球在原位置不动,使绳b在竖直平面内从水平方向逆时针转过θ角固定,绳b的拉力变为T2;再转过θ角固定,绳b的拉力为T3,则( )| A. | T1=T3>T2 | B. | T1<T2<T3 | C. | T1=T3<T2 | D. | T1>T2>T3 |
18. 如图所示,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直光滑杆上.当绳与竖直杆间的夹角为θ时,B沿杆下滑的速度为v,则下列判断正确的是( )
如图所示,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直光滑杆上.当绳与竖直杆间的夹角为θ时,B沿杆下滑的速度为v,则下列判断正确的是( )
 如图所示,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直光滑杆上.当绳与竖直杆间的夹角为θ时,B沿杆下滑的速度为v,则下列判断正确的是( )
如图所示,一条细绳跨过光滑轻定滑轮连接物体A、B,A悬挂起来,B穿在一根竖直光滑杆上.当绳与竖直杆间的夹角为θ时,B沿杆下滑的速度为v,则下列判断正确的是( )| A. | A的速度为vcosθ | B. | A的速度为vsinθ | ||
| C. | 细绳的张力一定大于A的重力 | D. | 细绳的张力一定小于A的重力 |
15.已知地球半径为R,质量为M,自转角速度为ω,万有引力恒量为G,地球同步卫星与地球表面之间的距离为h,下列计算正确的是( )
| A. | 地球近地卫星做匀速圆周运动的线速度为ωR | |
| B. | 地球近地卫星做匀速圆周运动的线速度为$\sqrt{\frac{GM}{R}}$ | |
| C. | 地球同步卫星的运行速度大小为ω(R+h) | |
| D. | 地球同步卫星的运行速度大小为$\sqrt{\frac{GM}{R+h}}$ |

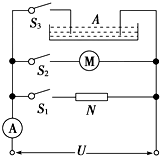 如图所示,A为电解槽,M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当S1闭合、S2、S3断开时,电流表A示数为6A;当S2闭合、S1、S3断开时,A示数为5A,且电动机输出功率为35W;当S3闭合、S1、S2断开时,A示数为4A.求:
如图所示,A为电解槽,M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当S1闭合、S2、S3断开时,电流表A示数为6A;当S2闭合、S1、S3断开时,A示数为5A,且电动机输出功率为35W;当S3闭合、S1、S2断开时,A示数为4A.求: 质量为1500kg 的汽车在平直的公路上运动,v-t图象如图所示.由此求:
质量为1500kg 的汽车在平直的公路上运动,v-t图象如图所示.由此求: