题目内容
15.已知地球半径为R,质量为M,自转角速度为ω,万有引力恒量为G,地球同步卫星与地球表面之间的距离为h,下列计算正确的是( )| A. | 地球近地卫星做匀速圆周运动的线速度为ωR | |
| B. | 地球近地卫星做匀速圆周运动的线速度为$\sqrt{\frac{GM}{R}}$ | |
| C. | 地球同步卫星的运行速度大小为ω(R+h) | |
| D. | 地球同步卫星的运行速度大小为$\sqrt{\frac{GM}{R+h}}$ |
分析 同步卫星的周期与地球自转周期相同,卫星绕地球做圆周运动万有引力提供圆周运动向心力.
解答 解:AB、近地卫星是在地球表面运行的人造卫星,轨道半径近似等于地球半径,研究近地卫星绕地球做匀速圆周运动,
根据万有引力提供向心力列出等式:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$,解得:v=$\sqrt{\frac{GM}{R}}$,故A错误,B正确;
C、同步卫星的角速度与地球自转角速度相同,同步卫星的轨道半径为(R+h),根据线速度与角速度的关系有线速度v=(R+h)ω,故C正确;
D、同步卫星绕地球做圆周运动的向心力由万有引力提供有:G$\frac{Mm}{(R+h)^{2}}$=m$\frac{{v}^{2}}{R+h}$,解得,同步卫星的速度:v=$\sqrt{\frac{GM}{R+h}}$,故D正确.
故选:BCD.
点评 本题考查了万有引力在天体中的应用,解题的关键在于找出向心力的来源,并能列出等式解题;万有引力定律得应用要结合圆周运动的知识解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.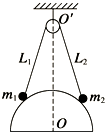 表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )
表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )
 表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )
表面光滑、半径为R的半球固定在水平地面上,球心O的正上方O′处有一无摩擦定滑轮,轻质细绳两端各系一个可视为质点的小球挂在定滑轮上,如图所示.两小球平衡时,若滑轮两侧细绳的长度分别为L1=2.4R和L2=2.5R,则这两个小球的质量之比为$\frac{{m}_{1}}{{m}_{2}}$,小球与半球之间的压力之比为$\frac{{N}_{1}}{{N}_{2}}$,则以下说法正确的是( )| A. | $\frac{{m}_{1}}{{m}_{2}}$=$\frac{24}{25}$ | B. | $\frac{{m}_{1}}{{m}_{2}}$=$\frac{25}{24}$ | C. | $\frac{{N}_{1}}{{N}_{2}}$=$\frac{25}{24}$ | D. | $\frac{{N}_{1}}{{N}_{2}}$=$\frac{24}{25}$ |
10.探究力对原来静止的物体做的功与物体获得的速度的关系,实验装置如图所示,实验主要过程如下: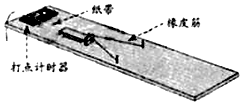
(1)设法让橡皮筋对小车做的功分别为W、2W、3W、…;
(2)分析打点计时器打出的纸带,求出小车的速度v1、v2、v3、…;
(3)作出W-v草图;
(4)分析W-v图象.如果W-v图象是一条直线,表明W∝v;如果不是直线,可考虑是否存在W∝v2、W∝v3、W∝$\sqrt{v}$等关系.
以下关于该实验的说法中有一项不正确,它是( )

(1)设法让橡皮筋对小车做的功分别为W、2W、3W、…;
(2)分析打点计时器打出的纸带,求出小车的速度v1、v2、v3、…;
(3)作出W-v草图;
(4)分析W-v图象.如果W-v图象是一条直线,表明W∝v;如果不是直线,可考虑是否存在W∝v2、W∝v3、W∝$\sqrt{v}$等关系.
以下关于该实验的说法中有一项不正确,它是( )
| A. | 本实验设法让橡皮筋对小车做的功分别为W、2W、3W、….所采用的方法是选用同样的橡皮筋,并在每次实验中使橡皮筋拉伸的长度保持一致.当用1条橡皮筋进行是实验时,橡皮筋对小车做的功为W,用2条、3条、…橡皮筋并在一起进行第2次、第3次、…实验时,橡皮筋对小车做的功分别是2W、3W、… | |
| B. | 小车运动中会受到阻力,补偿的方法,可以使木板适当倾斜 | |
| C. | 某同学在一次实验中,得到一条记录纸带.纸带上打出的点,两端密、中间疏.出现这种情况的原因,可能是没有使木板倾斜或倾角太小 | |
| D. | 根据记录纸带上打出的点,求小车获得的速度的方法,是以纸带上第一点到最后一点的距离来进行计算 |
20.下列的若干叙述中,正确的是( )
| A. | 黑体辐射电磁波的强度按波长的分布不只与黑体的温度有关,还与材料有关 | |
| B. | 对于同种金属产生光电效应时,逸出光电子的最大初动能 Ek与照射光的频率成线性关系 | |
| C. | 按照玻尔理论,氢原子核外电子从半径较小的轨道跃迁到半径较大的轨道时,电子的动能减小,原子的能量也减小了 | |
| D. | 将核子束缚在原子核内的核力,是不同于万有引力和电磁力的另一种相互作用 |
7.如图是A、B两物体同时由同一地点向同一方向做直线运动的v-t图象,从图象上可知( )
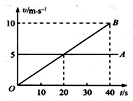

| A. | 20s末A、B相遇 | B. | A做匀速运动,B做匀加速运动 | ||
| C. | 20s末A、B相距最远 | D. | 40s末A、B相遇 |
4.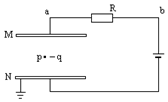 如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )
如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )
 如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )
如图所示,在水平放置两平行金属板M、N之间的P点,固定有一个带电量为-q的点电荷,两金属板通过电阻R接到直流电源上,其中N板接地.( )| A. | 当保持其它条件不变,而将M板向上移动的过程中,两极板间的电场变强 | |
| B. | 当保持其它条件不变,而将M板向上移动的过程中,通过R的电流方向是向左的 | |
| C. | 当保持其它条件不变,而将M板向上移动到某处稳定后与移动前相比,p处点电荷的电势能变大 | |
| D. | 将电容器与电源断开,若M板向上移动到某处稳定后与移动前相比,p处点电荷的电势能变小 |
5.一个固定的通电线圈L1电流方向如图所示,和一个可自由运动的线圈L2互相绝缘垂直放置,且两个线圈的圆心重合,则从左向右看,L2线圈作怎样的运动L2中才会产生感应电流( )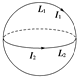

| A. | 不动 | B. | 顺时针转动 | C. | 逆时针转动 | D. | 在纸外平动 |
 如图所示某晚报道香港新建成的一种让人由落体的跳楼机.跳楼机先做自由落体运动,紧接着做匀减速运动,其中列出了一些数据供参考:总高度60m,限载12人;最大时速20m/s.根据以上信息估算:
如图所示某晚报道香港新建成的一种让人由落体的跳楼机.跳楼机先做自由落体运动,紧接着做匀减速运动,其中列出了一些数据供参考:总高度60m,限载12人;最大时速20m/s.根据以上信息估算: