题目内容
20. 动摩擦系数μ=0.2的水平地面AB长75m,和光滑斜面在B点用一小段光滑圆弧相连,斜面和水平地面的夹角为30°且无限长,一质量为m=1kg的物体(可视为质点)从A点以初速度v0=20m/s的速度向右滑动,滑上斜面后又下滑回到地面,最后停在地面AB上,求:
动摩擦系数μ=0.2的水平地面AB长75m,和光滑斜面在B点用一小段光滑圆弧相连,斜面和水平地面的夹角为30°且无限长,一质量为m=1kg的物体(可视为质点)从A点以初速度v0=20m/s的速度向右滑动,滑上斜面后又下滑回到地面,最后停在地面AB上,求:(1)物体经过B点时的速度大小;
(2)物体能上滑的最大高度.
(3)物体最后停在距离B点多远的地方;
(4)整个过程物块和地面的内能增加多少?
分析 (1)分析从A到B为物体受力情况,由动能定理可得到B点的速度大小,
(2)分析物体在斜面上受力情况,根据动能定理求解,
(3)通过(2)的分析结果确定,物块返回后的运动情况,再有动能定理求解即可,
(4)根据摩擦力做功表达式求解产生的热量,
解答 解:(1)物体运动过程中,受重力和支持力及向左的摩擦力,由动能定理可得:
-μmgLAB=$\frac{1}{2}$mvB2-$\frac{1}{2}$mv02,解得:vB=10m/s,
(2)物体在斜面上运动受重力和支持力,由动能定理可得:-mgh=$0-\frac{1}{2}m{v}_{B}^{2}$,解得:h=5m;
(3)物体在斜面上只有重力做功,当再次返回B点时速度相同仍为10m/s,在AB面上受重力和支持力,设在停在距离B点s远的地方,
在AB上运动时,由动能定理得:$0-\frac{1}{2}m{v}_{B}^{2}=-μmgs$,解得:s=25m,
(4)整个过程物块和地面的相对位移为,x=L+s=75+25=100m,
根据产生的热量等于摩擦力做功得:Q=Wf=μmghx=0.2×1×10×100=200J,
答:(1)物体经过B点时的速度大小为10m/s;
(2)物体能上滑的最大高度为5m.
(3)物体最后停在距离B点25m远的地方;
(4)整个过程物块和地面的内能增加200J.
点评 该题是比较简单的运动学和牛顿第二定律的结合题,但若是问第二次经过B的时间和速度,则该题的难度要增大一些,那样需要抓住物体在斜面上的运动过程是对称的这个特征来处理.

练习册系列答案
相关题目
12.“嫦娥三号”在环月圆轨道上做匀速圆周运动,向心力为F,动能为Ek;关于它们的变化情况,正确的是( )
| A. | F不变,Ek不变 | B. | F不变,Ek变化 | C. | F变化,Ek不变 | D. | F变化,Ek变化 |
15.在下列4个核反应方程中,X表示α粒子的是( )
| A. | ${\;}_{15}^{30}$P→${\;}_{14}^{30}$Si+X | B. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+X | ||
| C. | ${\;}_{13}^{27}$Al+X→${\;}_{12}^{27}$Mg+${\;}_{1}^{1}$H | D. | ${\;}_{13}^{27}$Al+X→${\;}_{15}^{30}$P+${\;}_{0}^{1}$n |
10. 如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
 如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )
如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运动的同时,吊钩将物体B向上吊起,A、B之间的距离以d=H-2t2(SI)(SI表示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做( )| A. | 速度大小不变的直线运动 | |
| B. | 速度大小增加的曲线运动 | |
| C. | 加速度大小方向均不变的曲线运动 | |
| D. | 加速度大小、方向均变化的曲线运动 |
 发电机模型.
发电机模型. 2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注.我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t,如图所示.已知月球半径为R,月球表面处重力加速度为g月,引力常量为G.
2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注.我国发射的“嫦娥三号”探月卫星在环月圆轨道绕行n圈所用时间为t,如图所示.已知月球半径为R,月球表面处重力加速度为g月,引力常量为G.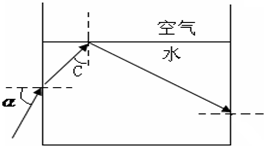 一束单色光由左侧射入存有清水的薄壁圆柱桶,图为过轴线的截面图,调整入射角α,光线恰好在空气和水界面上发生全反射,已知水的折射角为$\frac{4}{3}$
一束单色光由左侧射入存有清水的薄壁圆柱桶,图为过轴线的截面图,调整入射角α,光线恰好在空气和水界面上发生全反射,已知水的折射角为$\frac{4}{3}$