题目内容
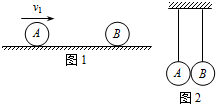 (1)如图1所示,光滑水平面上有两个小球A、B,A球以速度v1与原来静止的B球发生正碰,且碰撞过程中无机械能损失.设A球的质量为m1,B球的质量为m2.
(1)如图1所示,光滑水平面上有两个小球A、B,A球以速度v1与原来静止的B球发生正碰,且碰撞过程中无机械能损失.设A球的质量为m1,B球的质量为m2.a.求碰撞后它们的速度v1'和v2';
b.若A的初动能Ek1是一个定值,试论证当m1、m2满足什么关系时,A传给B的动能最少?
(2)如图2所示,将A、B球分别用等长的细线竖直悬挂起来,使它们刚好接触.悬点到球心的距离均为L.让B球静止在最低点,将A球向左拉起一个很小的偏角θ,然后释放,两球在最低点发生正碰且碰撞过程中无机械能损失.若m2=3m1,不考虑空气阻力的影响,释放A球时开始计时(t=0),求两球每次碰撞后的速度以及每次碰撞的时刻.
分析:(1)两球碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出两球碰撞后的速度;
由动能定理求出A对B做的功,然后由数学知识求出两物体质量满足什么关系时,A传给B的动能最少.
(2)两球碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出球的速度,两球做简谐运动,分析它们的运动过程,求出碰撞时间.
由动能定理求出A对B做的功,然后由数学知识求出两物体质量满足什么关系时,A传给B的动能最少.
(2)两球碰撞过程动量守恒、机械能守恒,由动量守恒定律与机械能守恒定律可以求出球的速度,两球做简谐运动,分析它们的运动过程,求出碰撞时间.
解答:解:(1)a、两个小球A、B发生弹性碰撞,动量守恒、机械能守恒,以A、B组成的系统为研究对象,A的初速度方向为正方向,由动量守恒得:
m1v1=m1v1′+m2v2′,
由机械能守恒定律得:
m1
=
m1v1′2+
m2v2′2,
解得碰撞后它们的速度:v1′=
v1,v2′=
v1;
b、对B,由动能定理得:Ek2=
m2v2′2=
m2(
v1)2=
?Ek1,
当 m1>>m2或 m1<<m2时,A传给B的动能最少;
(2)A球向下摆动的过程中,由机械能守恒定律得:
m1gL(1-cosθ)=
m1v12,
解得:v1=
;
以A、B组成的系统为研究对象,A的初速度方向为正方向,由动量守恒得:
m1v1=m1v1′+m2v2′,
由机械能守恒定律得:
m1
=
m1v1′2+
m2v2′2,
已知:m2=3m1,
解得A、B第一次碰撞后两球的速度:v1′=-
,v2′=
,
A、B第二次碰撞,由动量守恒定律得:m1
+3m1(-
)=m1v1″+3m1v2″,
由能量守恒定律得:
m1(
)2+
?3m1(-
)2=
m1v1″2+=
?3m1v2″2,
第二次碰撞后两球的速度:v1″=-v1,v1″=0;
第三次碰撞过程与第一次相同,第四次碰撞过程与第二次相同,…
第一次、第三次、第五次、…A、B碰撞后的速度:v1′=-
,v2′=
,
第二次、第四次、第六次、…A、B碰撞后的速度:v1″=-
,v2″=0,
单摆做简谐运动的周期:T=2π
,
两球发生碰撞的时刻:t=
+n
=(2n+1)
(其中n=0,1,2,3,…).
答:(1)a、两球碰撞后它们的速度分别为:v1′=
v1,v2′=
v1;
b、当 m1>>m2或 m1<<m2时,A传给B的动能最少.
(2)两球每次碰撞后的速度为:
第一次、第三次、第五次、…A、B碰撞后的速度:v1′=-
,v2′=
,
第二次、第四次、第六次、…A、B碰撞后的速度:v1″=-
,v2″=0,
每次碰撞的时刻为:t=
+n
=(2n+1)
(其中n=0,1,2,3,…).
m1v1=m1v1′+m2v2′,
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
解得碰撞后它们的速度:v1′=
| m1-m2 |
| m1+m2 |
| 2m1 |
| m1+m2 |
b、对B,由动能定理得:Ek2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2m1 |
| m1+m2 |
| 4 | ||||
|
当 m1>>m2或 m1<<m2时,A传给B的动能最少;
(2)A球向下摆动的过程中,由机械能守恒定律得:
m1gL(1-cosθ)=
| 1 |
| 2 |
解得:v1=
| 2gL(1-cosθ) |
以A、B组成的系统为研究对象,A的初速度方向为正方向,由动量守恒得:
m1v1=m1v1′+m2v2′,
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 1 |
| 1 |
| 2 |
| 1 |
| 2 |
已知:m2=3m1,
解得A、B第一次碰撞后两球的速度:v1′=-
| v1 |
| 2 |
| v1 |
| 2 |
A、B第二次碰撞,由动量守恒定律得:m1
| v1 |
| 2 |
| v1 |
| 2 |
由能量守恒定律得:
| 1 |
| 2 |
| v1 |
| 2 |
| 1 |
| 2 |
| v1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
第二次碰撞后两球的速度:v1″=-v1,v1″=0;
第三次碰撞过程与第一次相同,第四次碰撞过程与第二次相同,…
第一次、第三次、第五次、…A、B碰撞后的速度:v1′=-
| ||
| 2 |
| ||
| 2 |
第二次、第四次、第六次、…A、B碰撞后的速度:v1″=-
| 2gL(1-cosθ) |
单摆做简谐运动的周期:T=2π
|
两球发生碰撞的时刻:t=
| T |
| 4 |
| T |
| 2 |
| π |
| 2 |
|
答:(1)a、两球碰撞后它们的速度分别为:v1′=
| m1-m2 |
| m1+m2 |
| 2m1 |
| m1+m2 |
b、当 m1>>m2或 m1<<m2时,A传给B的动能最少.
(2)两球每次碰撞后的速度为:
第一次、第三次、第五次、…A、B碰撞后的速度:v1′=-
| ||
| 2 |
| ||
| 2 |
第二次、第四次、第六次、…A、B碰撞后的速度:v1″=-
| 2gL(1-cosθ) |
每次碰撞的时刻为:t=
| T |
| 4 |
| T |
| 2 |
| π |
| 2 |
|
点评:本题难度较大,是一道难题,分析清楚物体的运动过程是正确解题的关键,应用动能定律、动量守恒定律、机械能守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 (2011?辽宁二模)(1)如图1所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图2为xy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图2上x=0.4m处的Q点的说法正确的是
(2011?辽宁二模)(1)如图1所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图2为xy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图2上x=0.4m处的Q点的说法正确的是
 (1)如图1所示,一细束复色光(含红、蓝两种单色光)沿PO射向半圆形玻璃砖圆心O,观察到反射光线和折射光线分别为OQ、OR.下列判断不正确的是
(1)如图1所示,一细束复色光(含红、蓝两种单色光)沿PO射向半圆形玻璃砖圆心O,观察到反射光线和折射光线分别为OQ、OR.下列判断不正确的是