题目内容
 (2011?辽宁二模)(1)如图1所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图2为xy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图2上x=0.4m处的Q点的说法正确的是
(2011?辽宁二模)(1)如图1所示为波源的振动图象(在t=0时刻之前波源就已经开始振动了),图2为xy平面内沿x轴传播的简谐横波在t=0时刻的波形图象,t=0时刻P点向y轴负方向运动,关于图2上x=0.4m处的Q点的说法正确的是B
B
.(填入正确选项前的字母)A.t=0时,速度最大,其大小为0.1m/s,方向沿y轴正方向
B.t=0到t=5s内,通过的路程为20cm
C.t=2s时,运动到x=0.2m处
D.t=3s时,加速度最大,且方向向下
(2)桌面上有一玻璃圆锥,圆锥的轴(图中虚线)与桌面垂直,过轴线的截面为等边三角形,此三角形的边长为L,如图3所示,有一半径
| L |
| 3 |
| 3 |
①光在玻璃中的传播速度是多少?
②光束在桌面上形成的光斑的面积是多少?
分析:(1)由振动图象1读出周期,由波动图象2读出波长,求出波速.t=0时,Q点处于平衡位置速度最大,但其速度大小与波速大小不同.质点做简谐运动时,一个周期内通过的路程是四个振幅,根据时间与周期的关系,求解路程,确定Q的位移和加速度大小和方向.
(2)①由v=
求出光在玻璃中的传播速度.
②作出光路图,根据折射定律求出折射角,由几何关系求出光斑的直径,再求解其面积.
(2)①由v=
| c |
| n |
②作出光路图,根据折射定律求出折射角,由几何关系求出光斑的直径,再求解其面积.
解答:解:(1)A、由振动图象1读出周期为T=4s,由波动图象2读出波长为λ=0.4m,则波速为v=
=0.1m/s.由图2看出,t=0时,Q点处于平衡位置,速度最大,方向沿y轴正方向,但其速度大小与波速是两回事,不是0.1m/s,无法求出其速度大小.故A错误.
B、t=0到t=5s内,经历的时间为△t=1
T,Q点通过的路程为S=5A=20cm.故B正确.
C、t=2s时,Q点再次运动到平衡位置,x=0.故C错误.
D、t=3s时,Q点到达波谷,加速度最大,且方向向上.故D错误.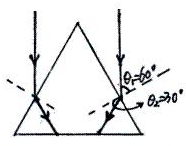
故选B
(2))①由v=
得,光在玻璃中的传播速度为v=
=
×108m/s
(2)作出光路图,如图所示.由几何知识得到:入射角θ1=60°,
根据折射定律得:n=
,代入解得,折射角θ2=30°.
由几何关系可知,产生的光斑直径为
,面积S=
π(
)2=
.
故答案为:
(1)B;
(2)①光在玻璃中的传播速度为
×108m/s;②光斑面积为
.
| λ |
| T |
B、t=0到t=5s内,经历的时间为△t=1
| 1 |
| 4 |
C、t=2s时,Q点再次运动到平衡位置,x=0.故C错误.
D、t=3s时,Q点到达波谷,加速度最大,且方向向上.故D错误.

故选B
(2))①由v=
| c |
| n |
| c | ||
|
| 3 |
(2)作出光路图,如图所示.由几何知识得到:入射角θ1=60°,
根据折射定律得:n=
| sinθ1 |
| sinθ2 |
由几何关系可知,产生的光斑直径为
| L |
| 3 |
| 1 |
| 4 |
| L |
| 3 |
| πL2 |
| 36 |
故答案为:
(1)B;
(2)①光在玻璃中的传播速度为
| 3 |
| πL2 |
| 36 |
点评:对于机械波,要把握质点的振动与波动之间的关系.几何光学作出光路图是解答的基础,要规范作出光路图,结合几何知识求解.

练习册系列答案
相关题目
 (2011?辽宁二模)如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞.已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力.求:
(2011?辽宁二模)如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞.已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力.求: (2011?辽宁二模)“探究功能与物体速度变化的关系”的实验装置如图所示.
(2011?辽宁二模)“探究功能与物体速度变化的关系”的实验装置如图所示. (2011?辽宁二模)甲、乙两物体在同一地点,沿同一直线运动,其速度--时间图象如图所示,则( )
(2011?辽宁二模)甲、乙两物体在同一地点,沿同一直线运动,其速度--时间图象如图所示,则( )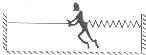 (2011?辽宁二模)运动员常利用如图所示的装置训练肌肉力量,弹簧右端与墙相连、左端系在运动员的腰上,左边墙上固定一根绳子.假定某运动员质量为50kg,他与地面间的动摩擦因数为μ=0.2,弹簧的劲度系数为k=1000N/m,运动员双手拉住绳子从弹簧原长位置向左缓慢前进(脚与地面间不打滑).当他向左运动的位移为3m时,运动员松开绳子被弹簧拉着向右滑行,若最大静摩擦力近似等于滑动摩擦力,g取10m/s2,则下列说法中不正确的是( )
(2011?辽宁二模)运动员常利用如图所示的装置训练肌肉力量,弹簧右端与墙相连、左端系在运动员的腰上,左边墙上固定一根绳子.假定某运动员质量为50kg,他与地面间的动摩擦因数为μ=0.2,弹簧的劲度系数为k=1000N/m,运动员双手拉住绳子从弹簧原长位置向左缓慢前进(脚与地面间不打滑).当他向左运动的位移为3m时,运动员松开绳子被弹簧拉着向右滑行,若最大静摩擦力近似等于滑动摩擦力,g取10m/s2,则下列说法中不正确的是( )