题目内容
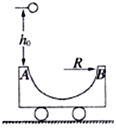
【题目】如图所示，质量为m的半圆轨道小车静止在光滑的水平地面上，其水平直径AB长度为2R。现将质量也为m的小球从距离A点正上方h0处由静止释放，然后由A点经过半圆轨道后从B点冲出，在空中能够上升的最大高度为
(不计空气阻力)，求：
(1)小车向左运动的最大距离；
(2)小车第二次能够上升的最大高度的范围。
【答案】（1）R（2）
【解析】解：（1）小球和小车组成的系统在水平方向动量守恒。设小球第一次离开半圆轨道时的水平速度为v，小车的速度为
，
由动量守恒定律得
设小球第一次进入半圆轨道至第一次离开半圆轨道所用时间为t，在这个过程中，小车的位移为x，取水平向右为正方向，则
解得 x=R
(2)设小球从开始下落到第一次上升到最大高度的过程中克服摩擦力坐的功为Wf，由动能定理得
解得 
由于第二次小球在车中运动时，在对应位置的速度小于第一次小球运动的速度，对应位置的摩擦力小于第一次所受的摩擦力，第二次在车中运动的过程中，克服摩擦力做的功
，机械能损失小于
设小球第二次上升的最大高度为
，由功和能的关系得
所以，小球第二次上升的最大高度范围是
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
