题目内容
如图所示,曲面PC和斜面PD固定在水平面MN上,C、D处平滑连接,O点位于斜面顶点P的正下方。某人从顶端P由静止开始分别沿曲面和斜面滑下,经过C、D两点后继续运动,最后停在水平面的A、B两处。各处材质相同,忽略空气阻力,则
A.此人在曲面PC和斜面PD上克服摩擦力做功一定相等
B.此人沿PCA和沿PDB运动克服摩擦力做功一定不相等
C.距离OA一定等于OB
D.距离OA一定小于OB
D
解析试题分析:设PD斜面与水平方向上的夹角为θ,
则PD段克服摩擦力做功Wf=μmgcosθs=μmgsPD水平。将PC段分成无数小段,由于在曲面上运动,径向的合力提供向心力,则支持力大于重力垂直于曲面方向上的分力,则每一小段克服摩擦力做功大于μmgscosα=μmgs水平,则整个曲面过程中,克服摩擦力做功大于μmgsPC水平.因为斜面和曲面的水平距离未知,则克服摩擦力做功不一定相等,A错误;对全过程运动动能定理得,mgh-Wf=0,知此人沿PCA和沿PDB运动克服摩擦力做功一定相等,B错误;因为整个过程克服摩擦力做功相等,沿斜面下滑在整个过程中摩擦力做功等于μmgsPB水平.而沿曲面下滑克服摩擦力做功大于μmgsPA水平,则OA一定小于OB,C错误,D正确。
考点:本题考查动能定理的应用。

 阅读快车系列答案
阅读快车系列答案如图所示,在竖直平面内有一个半径为R,粗细不计的圆管轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球恰能沿管道到达最高点B,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中
| A.重力做功2mgR |
| B.机械能减少mgR |
| C.合外力做功mgR |
D.克服摩擦力做功 mgR mgR |
某同学研究电子在电场中的运动时,电子仅受电场力作用,得到了电子由a点运动到b点的轨迹(虚线所示)图中一组平行实线可能是电场线,也可能是等势面,则下列说法正确的是
| A.不论图中实线是电场线还是等势面,a点的电势都比b点低 |
| B.不论图中实线是电场线还是等势面,a点的加速度都比b点小 |
| C.如果图中实线是电场线,电子在a点动能较小 |
| D.如果图中实线是等势面,电子在a点电势能较小 |
用长为l、不可伸长的细线把质量为m的小球悬挂于O点,将小球拉至悬线偏离竖直方向α角后放手,运动t时间后停在最低点。则在时间t内( )
| A.小球重力做功为mgl(1-cosα) |
| B.空气阻力做功为-mglcosα |
| C.小球所受合力做功为mglsinα |
D.绳拉力做功的功率为 |
阴极射线示波管的聚焦电场由电极A1、A2形成,实线为电场线,虚线为等势线,z轴为该电场的中心轴线,P、Q、R为一个从左侧进入聚焦电场的电子运动轨迹上的三点,则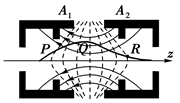
| A.电场中A2的电势高于电极A1的电势 |
| B.电场中Q点的电场强度小于R点的电场强度 |
| C.电子在P点处的动能大于Q点处的动能 |
| D.电子从P到R的运动过程中,电场力对它一直做正功 |
一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直向下。若不计空气阻力,则此带电油滴从a运动到b的过程中,能量变化情况为( )
| A.动能减小 |
| B.动能和电势能之和减小 |
| C.电势能增加 |
| D.重力势能和电势能之和增加 |
如图所示,质量为m的物体(可视为质点)以某一速度从A点冲上倾角为30°的固定斜面其运动的加速度大小为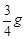 ,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )
,此物体在斜面上上升的最大高度为h,则在这个过程中物体( )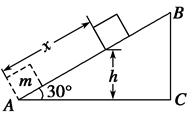
A.重力势能增加了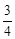 mgh mgh | B.克服摩擦力做功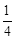 mgh mgh |
C.动能损失了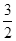 mgh mgh | D.机械能损失了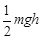 |
如图所示,木板OA水平放置,长为L,在A处放置一个质量为m的物体,现绕O点缓慢抬高到A处,直到当木板转到与水平面成α角时停止转动.这时物体因受到一个微小的干扰而开始缓慢匀速下滑,最后到达O点,则在整个过程中( )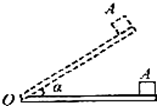
| A.支持力对物体做的总功为mgLsina |
| B.摩擦力对物体做的总功为零 |
| C.木板对物体做的总功为零 |
| D.木板对物体做的总功为正功 |
 ,物块落地时的速度大小为v,则
,物块落地时的速度大小为v,则




