题目内容
如图所示,在竖直平面内有一个半径为R,粗细不计的圆管轨道.半径OA水平、OB竖直,一个质量为m的小球自A正上方P点由静止开始自由下落,小球恰能沿管道到达最高点B,已知AP=2R,重力加速度为g,则小球从P到B的运动过程中
| A.重力做功2mgR |
| B.机械能减少mgR |
| C.合外力做功mgR |
D.克服摩擦力做功 mgR mgR |
B
解析试题分析:重力做功与路径无关,只与初末位置高度差有关,故WG=mgR,故A错误;小球恰能沿管道到达最高点B,得到B点速度为零,故小球从P到B的运动过程中,动能增加量为零,重力势能减小量为mgR,故机械能减少量为mgR,故B正确;小球从P到B的运动过程中,合外力做功等于动能的增加量,为零,故C错误;由B选项分析得到机械能减小量为mgR,而机械能减小量等于克服摩擦力做的功,故克服摩擦力做功为mgR,故D错误.
考点:功的计算,动能定理,功能关系

如图为一匀强电场,某带电粒子从A点运动到B点,在这一运动过程中克服重力做的功为2.0J,电场力做的功为1.5J,则下列说法正确的是( )
| A.粒子带负电 |
| B.粒子在A点的电势能比在B点少1.5J |
| C.粒子在A点的动能比在B点少0.5J |
| D.粒子在A点的机械能比在B点少1.5J |
如图所示,在皮带传送装置中,皮带把物体P匀速带至高处,在此过程中,下述说法正确的是( )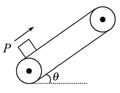
| A.摩擦力对物体做正功 |
| B.摩擦力对物体做负功 |
| C.支持力对物体不做功 |
| D.合外力对物体做正功 |
在奥运比赛项目中,高台跳水是我国运动员的强项。质量为60kg的跳水运动员进入水中后受到水的阻力做竖直向下的减速运动,设水对他的阻力大小恒为2600N,那么在他减速下降2m的过程中,下列说法正确的是(g =10m/s2)
| A.他的动能减少了5200J |
| B.他的重力势能减少了1200J |
| C.他的机械能减少了4000J |
| D.他的机械能保持不变 |
如图所示,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的小滑轮O,倾角为30°的斜面体置于水平地面上.A的质量为m,B的质量为3m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中,斜面体始终保持静止,下列判断中正确的是( )
| A.物块B受到的摩擦力先减小后增大 |
| B.地面对斜面体的摩擦力方向一直向右 |
| C.小球A所受重力的功率先增大后减小 |
| D.小球A的机械能先增大后减小 |
两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交PQ于O点,A点为MN上的一点。一带负电的试探电荷q,从A点由静止释放,只在静电力作用下运动.取无限远处的电势为零,则( )
| A.q由A向O做匀加速直线运动 |
| B.q由A向O运动的过程中电势能逐渐减小 |
| C.q运动到O点时的动能最小 |
| D.q运动到O点时电势能为零 |
在一场英超联赛中,我国球员孙继海大力踢出的球飞行15 m后,击在对方球员劳特利奇的身上.假设球击中身体时的速度约为22 m/s,离地高度约为1.5 m,估算孙继海踢球时脚对球做的功为
| A.15 J |
| B.150 J |
| C.1 500 J |
| D.15 000 J |

