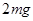题目内容
用长为l、不可伸长的细线把质量为m的小球悬挂于O点,将小球拉至悬线偏离竖直方向α角后放手,运动t时间后停在最低点。则在时间t内( )
| A.小球重力做功为mgl(1-cosα) |
| B.空气阻力做功为-mglcosα |
| C.小球所受合力做功为mglsinα |
D.绳拉力做功的功率为 |
A
解析试题分析:在t时间内,根据功的定义式可知,小球重力做的功为:WG=mgh=mgl(1-cosα),故选项A正确;根据功能关系可知,空气阻力做的功应等于小球减少的机械能,即:Wf=-mgh=-mgl(1-cosα),故选项B错误;根据动能定理可知,小球所受合力做的功等于其动能变化量,即为零,故选项C错误;由于小球释放后始终绕O点做圆弧轨迹运动,绳的拉力始终与速度垂直,因此不做功,即绳拉力做功的功率为零,故选项D错误。
考点:本题主要考查了动能定理、功能关系的应用问题,属于中档题。

 习题精选系列答案
习题精选系列答案两个带等量正电的点电荷,固定在图中P、Q两点,MN为PQ连线的中垂线,交PQ于O点,A点为MN上的一点。一带负电的试探电荷q,从A点由静止释放,只在静电力作用下运动.取无限远处的电势为零,则( )
| A.q由A向O做匀加速直线运动 |
| B.q由A向O运动的过程中电势能逐渐减小 |
| C.q运动到O点时的动能最小 |
| D.q运动到O点时电势能为零 |
如图所示,一固定斜面倾角为30°,一质量为m的小物块自斜面底端以一定的初速度沿斜面向上做匀减速运动,加速度大小等于重力加速度的大小g。物块上升的最大高度为H,则此过程中,物块的( )
| A.动能损失了2mgH | B.动能损失了mgH |
| C.机械能损失了mgH | D.机械能损失了 |
把导体匀速拉上斜面,如图所示,则下列说法正确的是(不计棒和导轨的电阻,且接触面光滑,匀强磁场磁感应强度B垂直框面向上)( )
| A.拉力做的功等于棒的机械能的增量 |
| B.拉力对棒做的功等于棒的动能的增量 |
| C.拉力与棒受到的磁场力的合力为零 |
| D.拉力对棒做的功与棒克服重力做的功之差等于回路中产生电能 |
如图所示,将一质量为m的小球从空中O点以速度v0水平抛出,飞行一段时间后,小球经过空间P点时动能为Ek ,不计空气阻力,则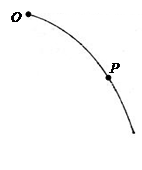
A.小球经过P点时竖直分速度为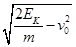 |
B.从O点到P点,小球的高度下降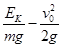 |
C.从O点到P点过程中,小球运动的平均速度为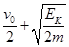 |
D.从O点到P点过程中,小球运动的平均速度为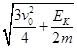 |
如图所示,甲、乙两种粗糙面不同的传送带,倾斜放于水平地面,与水平面的夹角相同,以同样恒定速率v向上运动。现将一质量为m的小物体(视为质点)轻轻放在A处,小物体在甲传送带上到达B处时恰好达到速率v;在乙上到达离B竖直高度为h的C处时达到速率v,已知B处离地面高度皆为H。则在物体从A到B过程中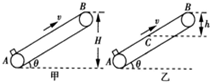
| A.小物块在两种传送带上具有的加速度相同 |
| B.将小物体传送到B处,两种传送带消耗的电能相等 |
| C.两种传送带对小物体做功相等 |
| D.将小物体传送到B处,两种系统产生的热量相等 |

 ,用丝线悬挂于O点,在竖直面内摆动,最大摆角为600,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,则小球自右方摆到最低点时悬线上的张力为 ( )
,用丝线悬挂于O点,在竖直面内摆动,最大摆角为600,水平磁场垂直于小球摆动的平面,当小球自左方摆到最低点时,悬线上的张力恰为零,则小球自右方摆到最低点时悬线上的张力为 ( )