题目内容
【题目】如图所示,质量为m=2 kg的木块在倾角θ=37°的斜面上由静止开始下滑,木块与斜面间的动摩擦因数为μ=0.5,已知:sin 37°=0.6,cos 37°=0.8,g取10 m/s2 . 求: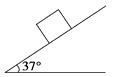
(1)前2 s内重力做的功;
(2)前2 s内重力的平均功率;
(3)2 s末重力的瞬时功率.
【答案】
(1)解:木块所受的合外力
F合=mgsin θ-μmgcos θ=mg(sin θ-μcos θ)=2×10×(0.6-0.5×0.8)N=4 N
木块的加速度a= ![]() =
= ![]() m/s2=2 m/s2
m/s2=2 m/s2
前2 s内木块的位移l= ![]() at2=
at2= ![]() ×2×22 m=4 m
×2×22 m=4 m
所以,重力在前2 s内做的功为W=mglsin θ=2×10×4×0.6 J=48 J
(2)解:重力在前2 s内的平均功率为![]() =
= ![]() =
= ![]() W=24 W
W=24 W
(3)解:木块在2 s末的速度
v=at=2×2 m/s=4 m/s
2 s末重力的瞬时功率P=mgvsin θ=2×10×4×0.6 W=48 W
【解析】此题属于基础题型,主要考查对于做功公式以及平均功率公式和瞬时功率公式的用法,答题时注意重力的方向和位移、速度的方向不同时利用夹角的三角函数进行求解。

练习册系列答案
相关题目