题目内容
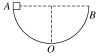
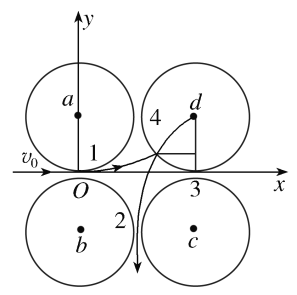
【题目】近代的材料生长和微加工技术,可制造出一种使电子的运动限制在半导体的一个平面内(二维)的微结构器件,且可做到电子在器件中像子弹一样飞行,不受杂质原子射散的影响.这种特点可望有新的应用价值.图甲所示为四端十字形,二维电子气半导体,当电流从1端进入时,通过控制磁场的作用,可使电流从2、3或4端流出.对下面模拟结构的研究,有助于理解电流在上述四端十字形导体中的流动.在图乙中,a、b、c、d为四根半径都为R的圆柱体的横截面,彼此靠得很近,形成四个宽度极窄的狭缝1、2、3、4,在这些狭缝和四个圆柱所包围的空间(设为真空)存在匀强磁场,磁场方向垂直于纸面向里.一个质量为m、电荷量为q的带正电的粒子,由静止经电场加速后,在纸面内以速度v0沿与a、b都相切的方向由缝1射入磁场内,与其中一个圆柱表面发生一次弹性碰撞(碰撞无机械能损失),从缝2处且沿与b、c都相切的方向射出,碰撞时间极短,且碰撞不改变粒子的电荷量,也不受摩擦力作用,重力忽略不计.加速电场两板间距为d,两极板厚度不计且其右极板与圆柱a、b同时相切.

(1)求加速电场电压U.
(2)求磁感应强度B.
(3)求从由静止加速到从缝2射出所用的时间t.
【答案】(1) ![]() (2)
(2) ![]()
(3)t=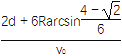 +
+![]()
【解析】(1)粒子由静止在电场中加速qU=![]() mv①
mv①
解得U=![]() ②
②
(2)在图中纸面内取Oxy坐标(如图),原点在狭缝1处,x轴过缝1和缝3.粒子从缝1进入磁场,在洛伦兹力作用下做圆周运动,圆轨道在原点与x轴相切,故其圆心必在y轴上.若以r表示此圆的半径,则圆方程为
x2+(r-y)2=r2③
根据题的要求和对称性可知,粒子在磁场中做圆周运动时应与d的柱面相碰于缝3、4间的圆弧中点处,碰撞处的坐标为x=2R-Rsin45°④
y=R-Rcos45°⑤
由③④⑤式,得r=3R⑥
由洛伦兹力和牛顿定律,有qv0B=m![]() ⑦
⑦
由⑥⑦式,得B=![]() ⑧
⑧
(3)在电场中加速用时t1=![]() ⑨
⑨
在磁场中转过两段圆弧,设每段圆弧对应圆心角为θ有
sinθ=![]() ⑩
⑩
且磁场中用时t2=![]()
t3=![]()
总共用时t=t1+t2+t3
由④⑨⑩式得t= +
+![]()