题目内容
【题目】如图所示，在xoy平面直角坐标系的第一象限有射线OA，OA与x轴正方向夹角为30°，OA与y轴所夹区域内有沿y轴负方向的匀强电场，其他区域存在垂直于坐标平面向外的匀强磁场．有一质量为m、电量为q的带正电粒子，从y轴上的P点沿着x轴正方向以初速度v0射入电场，运动一段时间后经过Q点垂直于射线OA进入磁场，经磁场偏转，过y轴正半轴上的M点再次垂直进入匀强电场．已知OQ=
h，不计粒子重力，求：
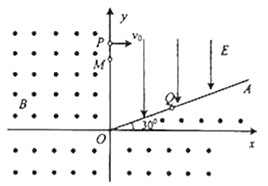
（1）粒子经过Q点时的速度大小；
（2）电场强度E和磁场磁感应强度B的大小；
（3）粒子从Q点运动到M点所用的时间．
【答案】（1）2v0；（2）
， 
；（3）
【解析】（1）粒子在电场中做类平抛运动，到达Q点时的速度：vQ=
=2v0；
（2）粒子在电场中做类平抛运动，
水平方向：OQcos30°=
hcos30°=v0t， 
，
竖直方向：vy=vQcos30°=
，解得： 
，
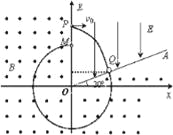
粒子在磁场中做匀速圆周运动，由几何知识得：r=OQ=
h
粒子在磁场中做匀速圆周运动，洛伦兹力提供向心力，
由牛顿第二定律得： 
，解得： 
；
（3）粒子在磁场中做圆周运动的周期： 
粒子在磁场中转过的圆心角：α=3600﹣（900﹣300）=3000
粒子从Q点运动到M点所用的时间： 
练习册系列答案
相关题目
