题目内容
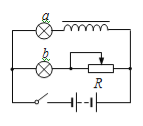
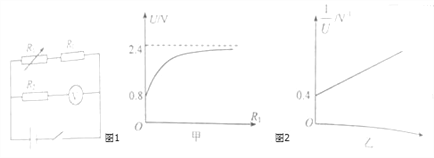
【题目】为测量一未知电源的电动势和内阻，某同学设计了如图所示电路，电路中所用到的器材规格如下：
待测电源：电动势约为4～6V，内阻约为几十欧姆；
定值电阻：R0=10Ω：
定值电阻：R2=3kΩ；
电阻箱R1：0～9999Ω；
电压表：量程0～3V，内阻Rv=3kΩ；
电键、导线若干
（1）闭合电键后，将电阻箱的阻值由零开始逐渐增大，记录若干组电阻箱R1和电压表的读数；
（2）第一次该同学将得到的数据在U﹣R1坐标系中描点连线，得到如图甲所示曲线，曲线与纵轴的截距为b1=0.8，虚数U=2.4为图中曲线的渐近线，由图可得电动势E=_____V，内阻r=____Ω；
（3）第二次该同学将得到的数据在
坐标系中描点连线，得到如图乙所示直线，直线与纵轴的截距为b2=0.4，斜率k=8.4，由图可得电动势E=___V，内阻r=___Ω；
（4）将两次数据处理方式进行对比，误差较小的应为第___次（填“一”或“二”）．
【答案】 （2）4.8； 20 （3）5.0， 21 （4）二
【解析】（2）根据闭合电路欧姆定律可知，当外电阻变大时，路端电压无限接近电动势，则可知，电动势
；
当外电阻为零时，路端电压U'= 
=1.6V，
则由闭合电路欧姆定律可知：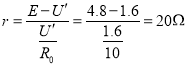 
；
（3）因路端电压U'=
=2U；则由闭合电路欧姆定律可知，2U=
（R1+R0）；变形可得： 
由图象规律可知， 
； 
解得；E=5.0V，r=21Ω；
（4）由于第一次实验中图象为曲线，只能利用渐近线和与纵轴的交点，第二次为直线，斜率及截距容易找到，能更有效的利用更多的数据，因此第二次误差较小；
练习册系列答案
阅读快车系列答案
相关题目
