题目内容
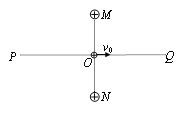
【题目】如图，虚线所示的圆形区域内存在一垂直于纸面的匀强磁场，P为磁场边界上的一点。大量相同的带电粒子以相同的速率经过P点，在纸面内沿不同的方向射入磁场。若粒子射入速率为
，这些粒子在磁场边界的出射点分布在六分之一圆周；若粒子射入速率为
，相应的出射点分布在四分之一圆周上。不计重力及带电粒子之间的相互作用。则
为
A. 
B. 
C. 
D. 
【答案】A
【解析】设圆形区域磁场的半径为r，当速度大小为v1时，从P点入射的粒子射出磁场时与磁场边界的最远交点为M(如图甲)时，
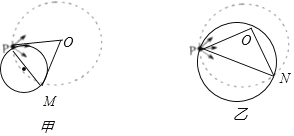
由题意知∠POM=60，由几何关系得轨迹圆半径为R1=r/2；
若粒子射入速率为
，从P点入射的粒子射出磁场时与磁场边界的最远交点为N(如图乙)；由题意知∠PON=90,由几何关系得轨迹圆的半径为R2= 
r；
根据洛伦兹力充当向心力可知：
解得： 
故速度与半径成正比,因此v1:v2=R1:R2 
故A正确，BCD错误。
故选：A.
根据题意画出带电粒子的运动轨迹，找出临界条件角度关系，利用圆周运动由洛仑兹力充当向心力，分别表示出圆周运动的半径，再由洛伦兹力充当向心力即可求得速度之比．
练习册系列答案
相关题目
