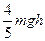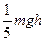题目内容
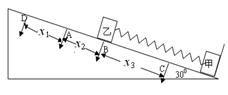
如图所示,倾角为θ=30°的光滑斜面固定在水平地面上,斜面底端固定一垂直斜面的挡板。质量为m=0.20kg的物块甲紧靠挡板放在斜面上,轻弹簧一端连接物块甲,另一端自由静止于A点,再将质量相同的物块乙与弹簧另一端连接,当甲、乙及弹簧均处于静止状态时,乙位于B点。现用力沿斜面向下缓慢压乙,当其沿斜面下降到C点时将弹簧锁定,A、 C两点间的距离为△L =0.06m。一个质量也为m的小球丙从距离乙的斜面上方L=0.40m处由静止自由下滑,当小球丙与乙将要接触时,弹簧立即被解除锁定。之后小球丙与乙发生碰撞(碰撞时间极短且无机械能损失),碰后立即取走小球丙。当甲第一次刚要离开挡板时,乙的速度为v=2.0m/s。(甲、乙和小球丙均可看作质点,g取10m/s2)求:
(1)小球丙与乙碰后瞬间乙的速度大小。
(2)从弹簧被解除锁定至甲第一次刚要离开挡板时弹簧弹性势能的改变量。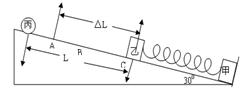
(1)小球丙与乙碰后瞬间乙的速度大小。
(2)从弹簧被解除锁定至甲第一次刚要离开挡板时弹簧弹性势能的改变量。

(1)2m/s(2)(3)0.08 J (减少量)
(1)对小球丙从顶端滑至乙处的过程,由动能定理得:
mgLsinθ=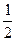 mv02
mv02
解得v0="2m/s " (5分)
对小球丙和乙的碰撞过程,由于二者碰撞过程时间极短,所以碰撞过程小球丙和乙组成的系统沿斜面方向动量守恒。又由于二者碰撞过程没有机械能损失,且小球丙和乙的质量相同,所以二者碰后交换速度,所以碰后乙的速度为:
v/=v0="2m/s" (10分)
(2)小球丙撤去后,乙先沿斜面向下运
动,速度为零后再沿斜面向上运动,当甲第
一次离开挡板时乙的速度为v=2m/s,设此时
乙的位置为D。可得乙在此过程中做简谐运
动,以B为平衡位置,C与D关于B对称。设D、A间距为x1,A、B间距为x2,B、C
间距为x3。则有:
x3=" x1+" x2
乙在B点时,对于乙,有:mgsinθ=k x1
乙在D点时,对于甲,有:mgsinθ=k x2
已知: x2 + x3 = △L (15分)
联立解得:x1= x2 ="0.02" m
x3="0.04m " (18分)
对于弹簧和乙组成的系统,从乙由C到D的过程中,由机械能守恒定律得:
△Ep弹 = △Ep乙= mg(x1+x2+ x3)sinθ=" 0.08J "
即该过程中弹簧弹性势能的改变量为0.08 J (减少量) (21分)

mgLsinθ=
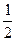 mv02
mv02 解得v0="2m/s " (5分)
对小球丙和乙的碰撞过程,由于二者碰撞过程时间极短,所以碰撞过程小球丙和乙组成的系统沿斜面方向动量守恒。又由于二者碰撞过程没有机械能损失,且小球丙和乙的质量相同,所以二者碰后交换速度,所以碰后乙的速度为:
v/=v0="2m/s" (10分)
(2)小球丙撤去后,乙先沿斜面向下运
动,速度为零后再沿斜面向上运动,当甲第
一次离开挡板时乙的速度为v=2m/s,设此时
乙的位置为D。可得乙在此过程中做简谐运
动,以B为平衡位置,C与D关于B对称。设D、A间距为x1,A、B间距为x2,B、C
间距为x3。则有:
x3=" x1+" x2
乙在B点时,对于乙,有:mgsinθ=k x1
乙在D点时,对于甲,有:mgsinθ=k x2
已知: x2 + x3 = △L (15分)
联立解得:x1= x2 ="0.02" m
x3="0.04m " (18分)
对于弹簧和乙组成的系统,从乙由C到D的过程中,由机械能守恒定律得:
△Ep弹 = △Ep乙= mg(x1+x2+ x3)sinθ=" 0.08J "
即该过程中弹簧弹性势能的改变量为0.08 J (减少量) (21分)

练习册系列答案
相关题目
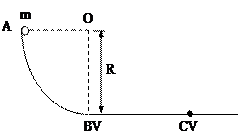
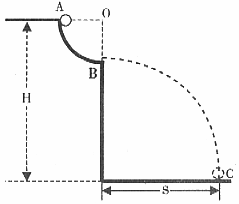
 圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴
圆弧,AC的竖直高度差h=0.45m。在紧靠管道出口D处有一水平放置且绕其水平中心轴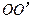 匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取
匀速旋转的圆筒,圆筒直径d=0.15m,桶上开有小孔E。现有质量为m=0.1kg且可视为质点的小球由静止开始从管口A滑下,小球滑到管道出口D处时,恰好能从小孔E竖直进入圆筒,随后,小球由小孔E处竖直向上穿出圆筒。不计空气阻力,取 。求:
。求: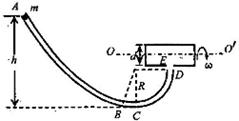


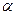 角(
角(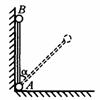
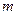 的物体,由静止开始下落,由于空气阻力,下落的加速度为
的物体,由静止开始下落,由于空气阻力,下落的加速度为 ,在物体下落
,在物体下落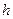 的过程中,下列说法错误的是( )
的过程中,下列说法错误的是( )