题目内容
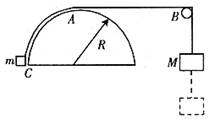
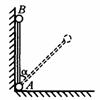
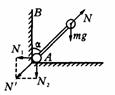
.如图所示,轻质细杆竖直位于相互垂直的光滑墙壁和光滑地板交界处,质量均为m的两个小球A与B固定在长度为L的轻质细杆两端,小球半径远小于杆长,小球A位于墙角处.若突然发生微小的扰动使杆沿同一竖直面无初速倒下,不计空气阻力,杆与竖直方向成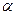 角(
角(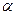 <arccos 2/3)时,求:
<arccos 2/3)时,求:
(1)球B的速度大小;
(2)球A对墙的弹力大小.
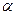 角(
角(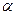 <arccos 2/3)时,求:
<arccos 2/3)时,求:(1)球B的速度大小;
(2)球A对墙的弹力大小.

(1)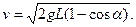 (2)
(2)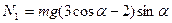
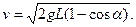 (2)
(2)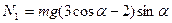
(1)如图所示,杆以球A为圆心,杆长L为半径做圆周运动,当杆与竖直方向或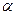 角时,球B的速度大小为v,根据机械能守恒定律得
角时,球B的速度大小为v,根据机械能守恒定律得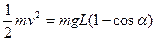 ,
,
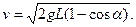
(2)对球B受力分析及应用牛顿第二定律得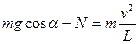 ,
,
设杆对小球A的弹力为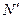 ,小球A对墙的弹力大小为Nl,则
,小球A对墙的弹力大小为Nl,则
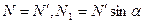 ,
,
解得球A对墙的弹力为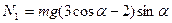 .
.
当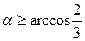 时,小球A离开墙角.
时,小球A离开墙角.
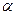 角时,球B的速度大小为v,根据机械能守恒定律得
角时,球B的速度大小为v,根据机械能守恒定律得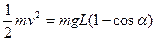 ,
,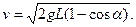
(2)对球B受力分析及应用牛顿第二定律得
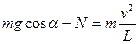 ,
,设杆对小球A的弹力为
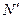 ,小球A对墙的弹力大小为Nl,则
,小球A对墙的弹力大小为Nl,则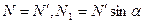 ,
,解得球A对墙的弹力为
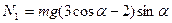 .
.当
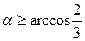 时,小球A离开墙角.
时,小球A离开墙角.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
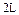 的轻杆上端及其正中央固定两个质量均为m的小球,杆的下端有光滑铰链与水平面相连接,杆原来竖直静止,现让其自由倒下,则A着地时的速度为( )
的轻杆上端及其正中央固定两个质量均为m的小球,杆的下端有光滑铰链与水平面相连接,杆原来竖直静止,现让其自由倒下,则A着地时的速度为( ) 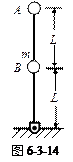
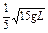
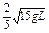
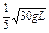
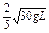
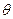

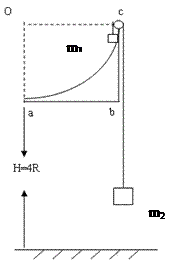
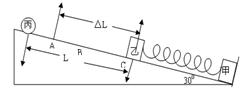
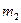 的左端,右端与小木块
的左端,右端与小木块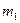 连接,且
连接,且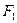 和
和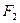 ,从两物体开始运动以后的整个过程中,对
,从两物体开始运动以后的整个过程中,对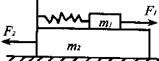
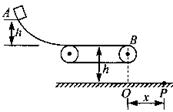
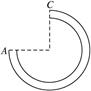
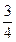 圆周细钢管,形状如图所示,A与圆心在同一水平面内,一小钢球被一弹簧枪从A处正对管口射入,射击时无机械能损失.第一种情况欲使小钢球恰能到达C点;第二种情况欲使钢球经C后飞出,恰好又落回A点,这两种情况下弹簧枪的弹性势能之比为________.
圆周细钢管,形状如图所示,A与圆心在同一水平面内,一小钢球被一弹簧枪从A处正对管口射入,射击时无机械能损失.第一种情况欲使小钢球恰能到达C点;第二种情况欲使钢球经C后飞出,恰好又落回A点,这两种情况下弹簧枪的弹性势能之比为________.