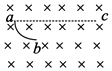��Ŀ����
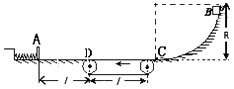
����Ŀ����ͼ������abcd�����дŸ�Ӧǿ��ΪB����ǿ�ų���ab�߳�Ϊ3L��bc���㹻������Ȳ��Ƶĵ���MN��Ϊ5L��ƽ��bc�߷����ڴų��У���bc�����L�������ab��Ҳ���L������Ϊm�������Ϊe�ĵ��ӣ��ɾ�ֹ��ʼ���糡���ٺ���ab�߽���ų��������뵲����ײ����ȫ�����ղ����ߣ�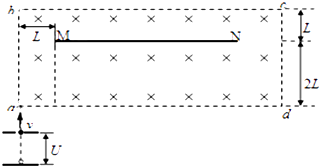
��1��������ٵ�ѹ������һ����Χ�ڣ��ܱ�֤�������ѹ��Χ�ڼ��ٵĵ��ӽ���ų����ڴų����˶�ʱ�䶼��ͬ����������ٵ�ѹU�ķ�Χ��
��2�����ڼ��ٵ�ѹ��ʹ���������ڵ����ϱ��棬��������ڵ����ϱ���������ȡ�L��
���𰸡�
��1���⣺�����ڴų����˶������������������������� ![]() �����ԣ������˶�����
�����ԣ������˶����� ![]() ��������ת�������Ľ���ͬ����ô�ڴų��е��˶�ʱ����ͬ��
��������ת�������Ľ���ͬ����ô�ڴų��е��˶�ʱ����ͬ��
�ɼ��ι�ϵ��֪��ֻ�е��Ӵ�ad���뿪�ų������˶��Ĺ켣Ϊ��Բ���˶�ʱ��ſ�����ͬ���Ҷ�Ϊ ![]() ��
��
�����Ӵ�ad���뿪�ų�ʱ�������˶��뾶0��R��2L��
�Ե����ڼ��ٵ糡���˶�Ӧ�ö��ܶ����ɵã��� ![]() ��
��
���ԣ� ![]() ��
��
���ԣ� ![]() ��
��
֮�����ٶ��������Ӵ���MN����������ƣ���ô���ĽǼ�С��
�����Ӿ���M��ʱ���ɼ��ι�ϵ�ɵã��뾶 ![]() �����Ӵ���MN�ϣ��ɼ��ι�ϵ�ɵã����Ӵ���MN�ϵĵ���M�ľ���L1=2��R1��L��=3L��
�����Ӵ���MN�ϣ��ɼ��ι�ϵ�ɵã����Ӵ���MN�ϵĵ���M�ľ���L1=2��R1��L��=3L��
���������ٶ����뾶����������ƣ���ʼ����MN�ϣ��������˶��켣��bc����ʱ�켣�뾶R2=3L���ɼ��ι�ϵ�ɵã� ![]() �������Ӵ���MN�ϣ�
�������Ӵ���MN�ϣ�
�ٶȼ����������Ӵ�bc�������������ƣ����ĽǼ�С����ֻ�����Ӵ�ad�����ʱ�ڴų��е��˶�ʱ��ſ�����ͬ��
��������ٵ�ѹ������һ����Χ�ڣ��ܱ�֤�������ѹ��Χ�ڼ��ٵĵ��ӽ���ų����ڴų����˶�ʱ�䶼��ͬ����ô������ٵ�ѹU�ķ�ΧΪ ![]() ��
��
��2���ɣ�1����֪�������˶��켣�Ӿ���M�㵽��bc���еķ�Χ���Ӵ��ڵ����ϱ��棻
�����Ӿ���M��ʱ���ɼ��ι�ϵ��֪���뾶 ![]() �����Ӵ���MN�ϵĵ���M�ľ���L1=2��R1��L��=3L��
�����Ӵ���MN�ϵĵ���M�ľ���L1=2��R1��L��=3L��
�������˶��켣��bc����ʱ�켣�뾶R2=3L�����Ӵ���MN�ϵĵ���M�ľ��� ![]() ��
��
���ԣ��������ڵ����ϱ���������� ![]()
�𣺵��ڼ��ٵ�ѹ��ʹ���������ڵ����ϱ��棬��������ڵ����ϱ���������ȡ�LΪ ![]() ��
��
����������1�����������ӣ�����ǿ�ų����˶����⣬����ȷ��Բ�ĵ�λ�ã�Ȼ����ݼ��Ϲ�ϵ������뾶��������ð뾶��ʽ��⡣������ֻ������뾶��Χ�����ݰ뾶��Χ����ٶȵķ�Χ���ɡ�
��2��������һ���еĽ��ۣ����ݼ��ι�ϵ����ʽ��⼴�ɡ�