题目内容
5.在一次抗洪抢险活动中,解放军某部动用直升飞机抢救落水人员,静止在空中的直升飞机上电动机通过悬绳将人从离飞机90m处的洪水中吊到机舱里.已知人的质量为80kg,吊绳的拉力不能超过1200N,电动机的最大输出功率为12kw,为尽快把人安全救起,操作人员采取的办法是:先让吊绳以最大拉力工作一段时间,而后电动机又以最大功率工作,当人到达机舱时恰好达到最大速度.(g=10m/s2)求:(1)人刚到达机舱时的速度;
(2)这一过程所用的时间.
分析 (1)吊绳先以最大的拉力工作,可知物体先做匀加速直线运动,当电动机达到最大功率,功率不变,速度增大,拉力减小,即物体做加速度减小的加速运动,当加速度减小到0,速度达到最大.所以拉力等于重力速度最大.
(2)全过程分两过程,第一阶段匀加速直线运动,根据匀变速运动求出时间,第二阶段加速度减小的加速运动,根据动能定理求出时间.
解答 解:(1)第一阶段以最大拉力拉着物体匀加速上升,当电动机达到最大功率时,
功率保持不变,物体变加速上升,速度增大,拉力减小,当拉力与重力相等时速度达到最大.
此时有:Pm=mgvm,代入数据解得:vm=$\frac{{P}_{m}}{mg}$=$\frac{12000W}{80kg×10m/{s}^{2}}$=15m/s,
此速度也是物体到达机舱的速度,故落水物体刚到达机舱时的速度为15m/s.
(2)对于第一段匀加速,加速度设为a,末速设为v1,上升高度h1,则有:
Fm-mg=ma,Pm=Fmv1,v1=a1t1,h1=$\frac{{v}_{1}}{2}$t1,代入数据解得:v1=10m/s,t1=2s,h1=10m;
第二段,以最大功率上升,由动能定理得:Pmt2-mg(h-h1)=$\frac{1}{2}$mvm2-$\frac{1}{2}$mv12,
代入数据解得:t2=5.75s,所以吊起落水物体所用总时间为:t=t1+t2=7.75s;
答:(1)人刚到达机舱时的速度为15m/s;
(2)这一过程所用的时间为7.75s.
点评 解决本题的关键知道工件在整个过程中的运动规律,对于求解变加速运动的时间,不能通过动力学知识求解,因为加速度在变化,抓住功率不变,运用动能定理进行求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.如图所示,A1、A2是完全相同的灯泡,线圈L的电阻可以忽略,下列说法中正确的是( )


| A. | 开关S接通时,A2灯先亮、A1灯逐渐亮,最后A1A2一样亮 | |
| B. | 开关S接通时,A1、A2两灯始终一样亮 | |
| C. | 断开S的瞬间,流过A2的电流方向与断开S前电流方向相反 | |
| D. | 断开S的瞬间,流过A1的电流方向与断开S前电流方向相反 |
19.两辆汽车在同一水平路面上行驶,它们的质量之比为m1:m2=1:2,速度之比为V1:V2=2:1.当汽车急刹车后,甲、乙两辆汽车滑行的最大距离为S1和S2,两车与路面的动摩擦因数相同,不计空气阻力,则( )
| A. | S1:S2=1:2 | B. | S1:S2=1:1 | C. | S1:S2=2:1 | D. | S1:S2=4:1 |
13.如图甲所示,理想变压器的原线圈电路中装有0.5A的保险丝L,原线圈匝数n1=600匝,副线圈匝数n2=120匝.当原线圈接在如图乙所示的交变电源上时,要使整个电路和用电器正常工作,则副线圈两端可以接( )


| A. | 阻值为14.4Ω的电阻 | B. | 并联两盏“36V,40W”的灯泡 | ||
| C. | 工作频率为10 Hz的电视 | D. | 耐压值为36V的电容器 |
20.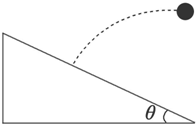 如图所示,以10m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上(g取10m/s2),可知物体完成这段飞行的时间是( )
如图所示,以10m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上(g取10m/s2),可知物体完成这段飞行的时间是( )
 如图所示,以10m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上(g取10m/s2),可知物体完成这段飞行的时间是( )
如图所示,以10m/s的水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角θ为30°的斜面上(g取10m/s2),可知物体完成这段飞行的时间是( )| A. | $\frac{\sqrt{3}}{3}$s | B. | $\frac{2\sqrt{3}}{3}$s | C. | $\sqrt{3}$s | D. | 2s |
10. 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
 如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )
如图所示,小球自a点由静止自由下落,到b点时与弹簧接触,到c点时弹簧被压缩到最短,若不计弹簧质量和空气阻力,在小球由a→b→c的运动过程中( )| A. | 小球的加速度先变小,后变大 | |
| B. | 小球经b点时动能最大 | |
| C. | 小球的机械能守恒 | |
| D. | 小球重力势能的减少量等于弹簧弹性势能的增加量 |
17.下列说法正确的是( )
| A. | 放射性元素的半衰期与外界的温度无关 | |
| B. | α、β和γ三种射线中,γ射线的穿透能力最强,电离能力也最强 | |
| C. | 比结合能越大的原子核越稳定 | |
| D. | 个别光子产生的效果往往显示粒子性,大量光子产生的效果往往显示波动性 |