题目内容
如图所示,在xOy平面内,第Ⅰ象限中有匀强电场,场强大小为E,方向沿x轴负方向,在第Ⅱ象限和第Ⅲ象限有匀强磁场,方向垂直于纸面向里.今有一个质量为m、,电荷量为e的质子(不计重力),从x轴上的P点以初速度v0垂直于电场方向进入电场.经电场偏转后,沿着与y轴正方向成45°角的方向进入磁场,从磁场中飞出时恰好能返回到原出发点P.试求:
(1)P点离坐标原点的距离l;
(2)磁场的磁感应强度B;
(3)质子第二次在电场中运动的时间t.
解:(1)质子运动轨迹如图所示.质子进入电场从P到A做类平抛运动,进入磁场从A到C再到D做匀速圆周运动,离开磁场从D到P做匀速直线运动.
质子经过A点的速度vA=v0/cos45°=
v0 ①
质子从P到A,由动能定理:qEl=
mvA2-
mv02 ②
解得l=
③
(2)设OA的距离为s1,OD的距离为s2,则s1=v0t ④
l=(v0tan45°)t/2 ⑤
解得s1=2l ⑥
质子从磁场中飞出时的方向与y轴亦成45°,所以s2=l ⑦
所以,质子在磁场中的轨迹半径为R=
⑧
由于R=
⑨
解得B=
⑩
(3)质子第二次在P点时,速度大小为
v0,速度方向与x轴正方向成45°.质子第二次在电场中运动,在x方向做初速度为v0、加速度大小为a=
的匀减速直线运动.
则有-l=v0t-
·
t2
解得t=(1+
)
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
（2013?安徽模拟）如图所示，在xoy平面上，直线OM与x轴正方向夹角为45°，直线OM左侧存在平行y轴的匀强电场，方向沿y轴负方向．直线OM右侧存在垂直xoy平面向里的磁感应强度为B的匀强磁场．一带电量为q质量为m带正电的粒子（忽略重力）从原点O沿x轴正方向以速度vo射入磁场．此后，粒子穿过磁场与电场的边界三次，恰好从电场中回到原点O．（粒子通过边界时，其运动不受边界的影响）试求：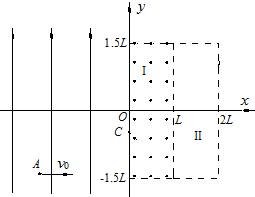
如图所示，在xOy平面的y轴左侧存在沿y轴正方向的匀强电场，y轴右侧区域Ⅰ内存在磁感应强度大小B1=
（2006?连云港二模）如图所示，在xoy平面上，一个以原点O为中心、半径为R的圆形区域内存在着一匀强磁场．磁场的磁感应强度为B，方向垂直于xoy平面向里．在O点处原来静止着一个具有放射性的原子核--氮（
如图所示，在xOy平面上，一个以原点O为圆心，半径为4R的原型磁场区域内存在着匀强磁场，磁场的方向垂直于纸面向里，在坐标（-2R，0）的A处静止着一个具有放射性的原子核氮713N．某时刻该核发生衰变，放出一个正电子和一个反冲核，已知正电子从A处射出时速度方向垂直于x轴，且后来通过了y轴，而反冲核刚好不离开磁场区域．不计重力影响和离子间的相互作用．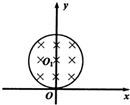
如图所示，在xOy平面上，以y轴上点Ol为圆心，半径为R=0.3m的圆形区域内，分布着一个方向垂直于xOy平面向里，磁感应强度大小为B=0.5T的匀强磁场．一个比荷