题目内容
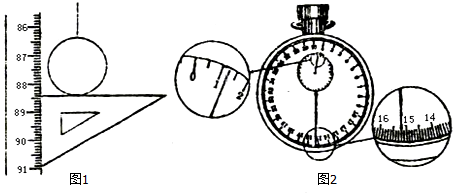
11.(1)某同学在做“利用单摆测重力加速度”实验中,用摆长l和周期T计算重力加速度的公式是g=$\frac{4{π}^{2}l}{{T}^{2}}$.如果已知摆球直径为2.00厘米,让刻度尺的零点对准摆线的悬点,摆线竖直下垂,如图1所示,那么单摆摆长是87.40cm.如果测定了40次全振动的时间如图2中秒表所示,秒表中秒针转动一周是30秒,那么秒表读数是75.2秒,单摆的摆动周期是1.88秒.(2)他测得的g值偏小,可能的原因是B
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了
C.开始计时时,秒表过迟按下
D.实验中误将39次全振动数为40次
分析 (1)根据单摆的周期公式得出重力加速度的表达式.摆长等于摆线的长度与摆球的半径之和,秒表的读数等于小盘读数加上大盘读数.
(2)根据重力加速度的表达式,结合周期和摆长的误差得出重力加速度的测量误差.
解答 解:(1)根据$T=2π\sqrt{\frac{l}{g}}$得,g=$\frac{4{π}^{2}l}{{T}^{2}}$,
摆长等于摆线的长度与摆球的半径之和,则摆长l=88.40cm-1.00cm=87.40cm,
秒表的读数为60s+15.2s=75.2s.
单摆的周期$T=\frac{75.2}{40}s=1.88s$.
(2)A、根据g=$\frac{4{π}^{2}l}{{T}^{2}}$知,测摆线长时摆线拉得过紧,摆长的测量值偏大,则重力加速度的测量值偏大,故A错误.
B、摆线上端未牢固地系于悬点,振动中出现松动,使摆线长度增加了,知摆长的测量值偏小,重力加速度测量值偏小,故B正确.
C、开始计时时,秒表过迟按下,则周期的测量值偏小,重力加速度的测量值偏大,故C错误.
D、实验中误将39次全振动数为40次,知周期的测量值偏小,重力加速度的测量值偏大,故D错误.
故选:B.
故答案为:(1)$\frac{4{π}^{2}l}{{T}^{2}}$,87.40cm,75.2,1.88,(2)B
点评 注意摆长等于单摆自然下垂时摆线的长度与摆球的半径之和、秒表的读数规则;灵活应用累积法测单摆的周期.

练习册系列答案
相关题目
1.在物理学发展史上伽利略、牛顿等许许多多科学家为物理学的发展做出了巨大贡献.以下选项中符合他们观点的是( )
| A. | 人在沿直线减速前进的火车车厢内,竖直向上跳起后,将落在起跳点的前方 | |
| B. | 两匹马拉车比一匹马拉车跑得快,这说明物体受的力越大速度就越大 | |
| C. | 速度越大的汽车越难以停下,这说明物体的惯性跟速度有关 | |
| D. | 一匹马拉着车前进,如果马不拉车,车最终将停下来,这说明“静止状态”才是物体不受力时的“自然状态” |
2.已知铜的摩尔质量为M(kg/mol),铜的密度为ρ(kg/m3),阿伏加德罗常数为NA(mol-1).下列判断错误的是( )
| A. | 1 kg铜所含的原子数为$\frac{{N}_{A}}{M}$ | B. | 1 m3铜所含的原子数为$\frac{M{N}_{A}}{ρ}$ | ||
| C. | 1个铜原子的质量为$\frac{M}{{N}_{A}}$(kg) | D. | 1个铜原子的体积为$\frac{M}{ρ{N}_{A}}$(m3) |
6.一个弹簧振子沿x轴做简谐振动,周期是1.0s.从经过平衡位置沿x轴正方向运动的时刻开始计时,那么经过1.2s后的时刻( )
| A. | 振子正在做加速运动,加速度正在增加 | |
| B. | 振子正在做加速运动,加速度正在减少 | |
| C. | 振子正在做减速运动,加速度正在增加 | |
| D. | 振子正在做减速运动,加速度正在减少 |
3. 如图所示,两个互相垂直的力F1和F2作用在同一物体上,使物体运动,物体发生一段位移后,力F1对物体做功为8J,力F2对物体做功为6J,则力F1与F2的合力对物体做功(总功)为
如图所示,两个互相垂直的力F1和F2作用在同一物体上,使物体运动,物体发生一段位移后,力F1对物体做功为8J,力F2对物体做功为6J,则力F1与F2的合力对物体做功(总功)为
( )
 如图所示,两个互相垂直的力F1和F2作用在同一物体上,使物体运动,物体发生一段位移后,力F1对物体做功为8J,力F2对物体做功为6J,则力F1与F2的合力对物体做功(总功)为
如图所示,两个互相垂直的力F1和F2作用在同一物体上,使物体运动,物体发生一段位移后,力F1对物体做功为8J,力F2对物体做功为6J,则力F1与F2的合力对物体做功(总功)为( )
| A. | 10J | B. | 14J | C. | 2J | D. | 7J |
20.交流发电机工作时产生的感应电动势的最大值为Em,周期为T;若使其电枢的转速提高一倍,其它条件不变,其电动势的最大值Em′和周期T′为( )
| A. | Em′=Em | B. | Em′=2Em | C. | T′=T | D. | T′=2T |
1.高三某同学对自己在本学期学校体检后的一些数据在单位上作了一些转化,其中部分数据在如下选项中给出,在他给出的数据中,属于国际单位制中基本单位的是( )
| A. | 体重G=637N | B. | 质量m=65kg | C. | 身高H=178cm | D. | 血压115/75mmHg |

 一列横波沿x轴传播,波速v=50m/s.已知t=0时刻的波形如图所示.图中M点正经过平衡位置沿y轴正方向运动.
一列横波沿x轴传播,波速v=50m/s.已知t=0时刻的波形如图所示.图中M点正经过平衡位置沿y轴正方向运动.