题目内容
质量为m、电量为q的质点,在静电力作用下以恒定速率v沿圆弧从A点运动到B点,其速度方向改变的角度为θ(弧度),AB弧长为s。则A,B两点间的电势差ΦA-ΦB=_____,AB弧中点场强大小E=_____。
0、mv2θ/qs
由题意知电荷在静电力作用下做的是匀速圆周运动,从A点运动到B点,由动能定理知,静电力做的功是零,所以A、B两点间的电势差UAB=0(也可根据圆周是等势线判断);设场源电荷的电荷量为Q,质点做圆周运动的轨道半径为r,则弧长s=θr ①
静电力是质点做圆周运动的向心力,即
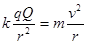 ②
②
弧AB中点的场强大小E=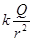 ③
③
解①②③组成的方程组得:E=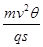
静电力是质点做圆周运动的向心力,即
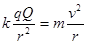 ②
②弧AB中点的场强大小E=
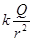 ③
③解①②③组成的方程组得:E=
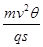

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


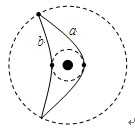


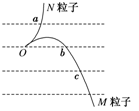
 >0的空间中,存在沿x轴正方向的匀强电场
>0的空间中,存在沿x轴正方向的匀强电场 ;在
;在 处的
处的 点以沿
点以沿 轴正方向的初速度
轴正方向的初速度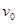 开始运动,电子所受重力不计,求:
开始运动,电子所受重力不计,求:
