Question

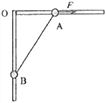
【题目】如图所示，O点距水平地面的高度为H=3m，不可伸长的细线一端固定在O点另一端系一质量m=2kg的小球（可视为质点），另一根水平细线一端固定在墙上A点，OB线与竖直方向的夹角为37o，l<H, g取10m/s2, 空气阻力不计. (sin370=0.6，cos370=0.8，)

（1）若OB的长度l=1m ,剪断细线AB的同时,在竖直平面内垂直OB的方向上,给小球一个斜向下的冲量,为使小球恰好能在竖直平面内做完整的圆周运动,求此冲量的大小；

（2）若先剪断细线AB,当小球由静止运动至最低点时再瞬间断开OB,小球最终落地,求OB的长度l为多长时,小球落地点与O点的水平距离最远,最远水平距离是多少.

Answer 1

【答案】（1）2kgm/s（2）

【解析】

（1）要使小球恰好能在竖直平面内做完整的圆周运动，最高点需满足临界条件，再根据动能定理可得一开始的冲量大小；

（2）最低点剪断绳子后小球做平抛运动，利用相关知识可得平抛水平距离与绳长的关系，用函数知识分析最大值。

（1）要使小球恰好能在竖直平面内做完整的圆周运动，最高点需满足：

①

写出从B点到最高点的动能定理：②

联立得一开始的冲量

（2）从B点剪断绳子到小球至最低点用机械能守恒可得

小球从H-l高度做初速度为v0的平抛运动，

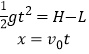
联立得，

L=1.5m时x取最大值，为