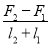题目内容
11. 如图所示,长为L的轻质细线,一端固定在O点,另一端栓一质量为m的小球,让小球在空中某水平面内做匀速圆周运动,运动过程中O点与该水平面之间的距离为h,已知重力加速度为g,求:
如图所示,长为L的轻质细线,一端固定在O点,另一端栓一质量为m的小球,让小球在空中某水平面内做匀速圆周运动,运动过程中O点与该水平面之间的距离为h,已知重力加速度为g,求:(1)细线对小球的拉力大小;
(2)小球做圆周运动的周期.
分析 小球在重力和拉力合力作用下做圆周运动,靠两个力的合力提供向心力,根据牛顿第二定律求出角速度,进而求出周期.
解答 解:(1)设运动过程中细线与竖直方向的夹角为θ,
由题意可知cosθ=$\frac{h}{L}$
细线对小球的拉力大小为F=$\frac{mg}{cosθ}$=$\frac{mgL}{h}$;
(2)由牛顿第二定律可得:mgtanθ=mω2Lsinθ
周期和角速度的关系为:T=$\frac{2π}{ω}$
解得:T=2π$\sqrt{\frac{h}{g}}$.
答:(1)细线对小球的拉力大小为$\frac{mgL}{h}$;
(2)小球做圆周运动的周期是2π$\sqrt{\frac{h}{g}}$.
点评 解决本题的关键搞清小球做圆周运动向心力的来源,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
19.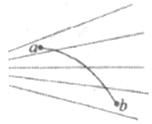 如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
 如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )
如图所示,实线是一带电粒子仅在电场力作用下由a点运动到b点的运动轨迹,虚线是电场线,则( )| A. | 粒子在a点的加速度一定小于在b点的加速度 | |
| B. | 粒子在a点的动能大于b点的动能 | |
| C. | 粒子在a点的电势能大于b点的电势能 | |
| D. | a点的电势一定高于b点的电势 |
6.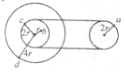 如图所示为一皮带传动装置,右轮半径为2r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则( )
如图所示为一皮带传动装置,右轮半径为2r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则( )
 如图所示为一皮带传动装置,右轮半径为2r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则( )
如图所示为一皮带传动装置,右轮半径为2r,a是它边缘上的一点.左侧是一轮轴,大轮的半径为4r,小轮的半径为2r.b点在小轮上,到轮中心的距离为r.c点和d点分别位于小轮和大轮的边缘上.若传动过程中皮带不打滑,则( )| A. | a点与b点的线速度大小相等 | B. | a点与b点的角速度大小相等 | ||
| C. | a点与c点的线速度大小相等 | D. | a点与d点的向心加速度大小相等 |
15.以下关于玻尔原子理论的说法中正确的是( )
| A. | 电子绕原子核做圆周运动的轨逍半径可以取任意值 | |
| B. | 电子在绕原子核做圆周运动时,稳定地产生电磁辐射 | |
| C. | 电子从量子数为2的能级跃迁到量子数为3的能级时要辐射光子 | |
| D. | 不同频率的光照射处于基态的氢原子时,只有某些频率的光子可以被氢原子吸收 |
1.关于电阻、电感、电容对电流作用的说法正确的是( )
| A. | 电感线圈对交流电的阻碍作用是由于线圈自身存在电阻 | |
| B. | 电阻对直流电和交流电的阻碍作用相同 | |
| C. | 感抗、容抗和电阻一样,电流通过它们做功时都是电能转化为内能 | |
| D. | 交变电流的频率增加时,电阻、电感线圈、电容器对电流的阻碍作用都增强 |
17.关于物理学史,下列说法正确的是( )
| A. | 亚里士多德认为力是改变物体运动状态的原因 | |
| B. | 伽利略利用扭秤实验成功地测出了引力常量 | |
| C. | 牛顿通过斜面实验直接得出了牛顿第一定律 | |
| D. | 开普勒通过对其导师第谷关于行星运动的观测数据的研究,得出了开普勒行星运动定律 |
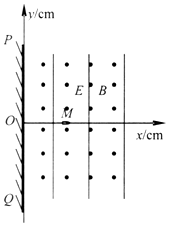 如图所示,在坐标系xOy平面的x>0区域内,存在电场强度大小E=2×105N/C、方向垂直于x轴的匀强电场和磁感应强度大小B=0.20T、方向与xOy平面垂直向外的匀强磁场.在y轴上有一足够长的荧光屏PQ,在x轴上的M(10,0)点处有一粒子发射枪向x轴正方向连续不断地发射大量质量m=6.4×10-27kg、电荷量q=3.2×10-19C的带正电粒子(重力不计),粒子恰能沿x轴做匀速直线运动.若撤去电场,并使粒子发射枪以M点为轴在xOy平面内以角速度ω=2πrad/s顺时针匀速转动(整个装置都处在真空中).
如图所示,在坐标系xOy平面的x>0区域内,存在电场强度大小E=2×105N/C、方向垂直于x轴的匀强电场和磁感应强度大小B=0.20T、方向与xOy平面垂直向外的匀强磁场.在y轴上有一足够长的荧光屏PQ,在x轴上的M(10,0)点处有一粒子发射枪向x轴正方向连续不断地发射大量质量m=6.4×10-27kg、电荷量q=3.2×10-19C的带正电粒子(重力不计),粒子恰能沿x轴做匀速直线运动.若撤去电场,并使粒子发射枪以M点为轴在xOy平面内以角速度ω=2πrad/s顺时针匀速转动(整个装置都处在真空中).
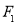 的力压弹簧的另一端,平衡时长度为
的力压弹簧的另一端,平衡时长度为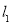 ;改用大小为
;改用大小为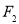 的力拉弹簧,平衡时长度为
的力拉弹簧,平衡时长度为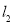 。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为
。弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为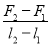 B.
B.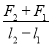 C.
C.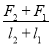 D.
D.